题目内容
(1)图1是某同学在做匀变速直线运动实验中获得的一条纸带.
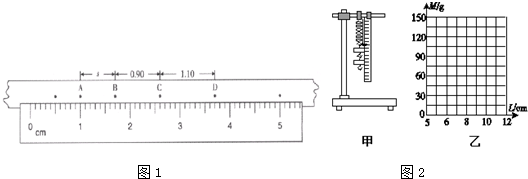
①已知打点计时器电源频率为50Hz,A、B、C、D是纸带上四个计数点,每两个相邻计数点间有四个点没有画出.从图中读出A、B两点间距s=
②如果当时电网中交变电流的频率实际是f=51Hz,而做实验的同学并不知道,那么加速度的测量值与实际值相比
(2)要测量某导电材料棒的电阻.
①首先用多用电表的欧姆档(倍率为×100)粗测其电阻,指针位置如图2(a)所示,其读数为
②然后用以下器材用伏安法尽可能精确地测量其电阻:
A.电流表:量程为0-5mA-25mA,5mA内阻约为10Ω,25mA内阻约为2Ω
B.电压表:量程为0-3V-15V,3V内阻约为7.2kΩ,15V内阻约为36kΩ
C.滑动变阻器:最大阻值为20Ω,额定电流1A
D.低压直流电源:电压4V,内阻可以忽略
E.电键K,导线若干
按提供的器材,要求测量误差尽可能小,在下面实物图2(b)上连接正确的实验电路.
③根据实验的测量数据在坐标系中描点,如图2(c)所示.
请在图(c)中作出该导电材料棒的伏安特性曲线,则其阻值为

①已知打点计时器电源频率为50Hz,A、B、C、D是纸带上四个计数点,每两个相邻计数点间有四个点没有画出.从图中读出A、B两点间距s=
0.70cm
0.70cm
;C点对应的速度是0.100m/s
0.100m/s
(计算结果保留三位有效数字).②如果当时电网中交变电流的频率实际是f=51Hz,而做实验的同学并不知道,那么加速度的测量值与实际值相比
偏小
偏小
(选填:偏大、偏小或不变).(2)要测量某导电材料棒的电阻.
①首先用多用电表的欧姆档(倍率为×100)粗测其电阻,指针位置如图2(a)所示,其读数为
900
900
Ω.②然后用以下器材用伏安法尽可能精确地测量其电阻:
A.电流表:量程为0-5mA-25mA,5mA内阻约为10Ω,25mA内阻约为2Ω
B.电压表:量程为0-3V-15V,3V内阻约为7.2kΩ,15V内阻约为36kΩ
C.滑动变阻器:最大阻值为20Ω,额定电流1A
D.低压直流电源:电压4V,内阻可以忽略
E.电键K,导线若干
按提供的器材,要求测量误差尽可能小,在下面实物图2(b)上连接正确的实验电路.
③根据实验的测量数据在坐标系中描点,如图2(c)所示.
请在图(c)中作出该导电材料棒的伏安特性曲线,则其阻值为
810
810
Ω.
分析:(1)根据相等时间内位移之差相等,可求出AB间距;打点计时器打点周期与交变电流的周期相同.由t=5×0.02s,算出计数点间的时间隔T,BD间平均速度近似等于C点的速度.由△x=aT2求加速度a=
式中代入计算的T比实际T大,导致加速度变小.
(2)①欧姆表读数=表盘读数×倍率
②计算出电路中的电流和电压,然后在不超过量程的前提下,尽量选择电流表和电压表的小量程;
需要较大的电压测量范围,故滑动变阻器采用分压式接法;由于电阻值较大,“大外小内”,需要选择安培表内接法.
③根据伏安特性曲线即可求解电阻阻值.
| △x |
| T2 |
(2)①欧姆表读数=表盘读数×倍率
②计算出电路中的电流和电压,然后在不超过量程的前提下,尽量选择电流表和电压表的小量程;
需要较大的电压测量范围,故滑动变阻器采用分压式接法;由于电阻值较大,“大外小内”,需要选择安培表内接法.
③根据伏安特性曲线即可求解电阻阻值.
解答:解:(1)①带上打相邻两点的时间间隔T=
=
s=0.02s
②B、C间的距离为0.90cm、C、D间的距离1.10cm、由于它们的时间相等,则位移之差应该相等,即为1.10-0.90=0.90-SAB,则A、B间的距离SAB=0.70cm.
③B、D间的时间间隔T=0.1s
则vc=
=
cm/s=0.100m/s
由△x=aT2求加速度a=
式中代入计算的T比实际T大,导致加速度变小.
(2)
①欧姆表读数=表盘读数×倍率=9×100Ω=900Ω
②根据估测电阻与电流表及电压表阻值相比,待测电阻偏大,故选择电流表内接法;
而滑动变阻器的电阻与待测电阻相差太大,故选择分压式接法.电路图如图所示

③将该导电材料棒的伏安特性曲线平滑连接,出现过原点的一条倾斜直线.
再根据电阻定律,有R=
,在图象上确定一点,则有:R=
Ω=810Ω
故答案为:(1)①0.70cm 0.100m/s; ②偏小.
(2)①900Ω
②如图.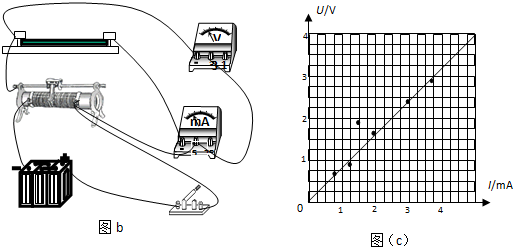
③特性曲线如图,800Ω(780Ω-820Ω)
| 1 |
| f |
| 1 |
| 50 |
②B、C间的距离为0.90cm、C、D间的距离1.10cm、由于它们的时间相等,则位移之差应该相等,即为1.10-0.90=0.90-SAB,则A、B间的距离SAB=0.70cm.
③B、D间的时间间隔T=0.1s
则vc=
| xBD |
| 2T |
| 0.9+1.1 |
| 2×0.1 |
由△x=aT2求加速度a=
| △x |
| T2 |
(2)
①欧姆表读数=表盘读数×倍率=9×100Ω=900Ω
②根据估测电阻与电流表及电压表阻值相比,待测电阻偏大,故选择电流表内接法;
而滑动变阻器的电阻与待测电阻相差太大,故选择分压式接法.电路图如图所示

③将该导电材料棒的伏安特性曲线平滑连接,出现过原点的一条倾斜直线.
再根据电阻定律,有R=
| U |
| I |
| 3.24 |
| 4×10-3 |
故答案为:(1)①0.70cm 0.100m/s; ②偏小.
(2)①900Ω
②如图.

③特性曲线如图,800Ω(780Ω-820Ω)
点评:打点计时器问题常常根据匀变速运动的推论:由vn=
求解速度,由△x=aT2求加速度.
同时本题关键是:(1)会读欧姆表的读数;(2)明确伏安法测电阻的实验原理和误差来源,能够选择合适的连接方法减小误差.
| xn+xn+1 |
| 2T |
同时本题关键是:(1)会读欧姆表的读数;(2)明确伏安法测电阻的实验原理和误差来源,能够选择合适的连接方法减小误差.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
(1)图1是某同学在做研究匀变速直线运动实验中获得的一条纸带.
①已知打点计时器电源频率为50Hz,A、B、C、D是纸带上四个计数点,每两个相邻计数点间有四个点没有画出.从图1中读出A、B两点间距s=______;C点对应的速度是______ (计算结果保留三位有效数字).
②如果当时电网中交变电流的频率实际是f=51Hz,而做实验的同学并不知道,那么加速度的测量值与实际值相比______(选填:偏大、偏小或不变).
(2)某同学在做探究弹力和弹簧伸长的关系的实验时,设计了如图2甲所示的实验装置.所用的钩码的质量都是30g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中.(弹力始终未超过弹性限度,取g=10m/s2)
①试根据这些实验数据,在图2乙所示的坐标纸上作出砝码质量M与弹簧总长度L之间的函数关系图线.
②上一问所得图线的物理意义是:______
③该弹簧劲度系数k=______ N/m.(结果保留两位有效数字)

①已知打点计时器电源频率为50Hz,A、B、C、D是纸带上四个计数点,每两个相邻计数点间有四个点没有画出.从图1中读出A、B两点间距s=______;C点对应的速度是______ (计算结果保留三位有效数字).
②如果当时电网中交变电流的频率实际是f=51Hz,而做实验的同学并不知道,那么加速度的测量值与实际值相比______(选填:偏大、偏小或不变).
(2)某同学在做探究弹力和弹簧伸长的关系的实验时,设计了如图2甲所示的实验装置.所用的钩码的质量都是30g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中.(弹力始终未超过弹性限度,取g=10m/s2)
| 砝码质量M(g) | 30 | 60 | 90 | 120 | 150 | |
| 弹簧总长L(cm) | 6.00 | 7.15 | 8.34 | 9.48 | 10.64 | 11.79 |
②上一问所得图线的物理意义是:______
③该弹簧劲度系数k=______ N/m.(结果保留两位有效数字)


 ①在图2(b)的实物图中,已正确连接了部分电路,请完成余下电路的连接.
①在图2(b)的实物图中,已正确连接了部分电路,请完成余下电路的连接.