Question

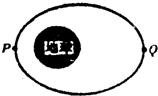如图所示，人造地球卫星绕地球运行轨道为椭圆，其近地点P和远地点Q距地面的高度分别为R和3R，R为地球半径，已知地球表面处的重力加速度为g，以下说法正确的是（　　）

• A．卫星在P点的速度等于

  gR 2

• B．卫星在Q点的加速度等于

  g

  4

• C．卫星在从P到Q过程中处于超重状态
• D．卫星在从P到Q过程中机械能守恒

Answer 1

分析：万有引力大于该点所需的向心力会做近心运动，万有引力小于该点所需的向心力会做离心运动．
根据卫星所受的万有引力比较加速度大小．
根据影响动能和重力势能大小的因素来分析动能和重力势能的变化，动能和势能统称为机械能．

解答：解：A、若卫星在离地面R处做匀速圆周运动，根据万有引力提供向心力G

Mm

(2R)2

=m

v2

2R

，得v=

GM 2R

．又因为地面重力等于万有引力mg=

GM

R2

，所以v=

gR 2

．人造地球卫星在P点的速度必须大于

gR 2

，万有引力不够提供向心力而做离心运动，才能绕地球做椭圆轨道运行．故A错误．
B、卫星在Q点受到的万有引力为G

Mm

(4R)2

=ma，所以a=

1

16

GM

R2

，而在地面处mg=

GMm

R2

，所以a=

g

16

．故B错误．
C、根据开普勒第二定律可知，卫星在近地点速度大，在远地点速度小，即卫星在从P到Q过程中，做向上的减速运动，处于失重状态．故C错误．
D、卫星在从P到Q过程中，只有地球的引力作用，故机械能守恒，故D正确．
故选：D．

点评：解决此题要知道人造地球卫星在近地点速度最大，动能最大，势能最小；在远地点势能最大，动能最小，速度最小．