题目内容
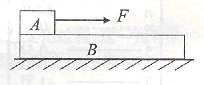
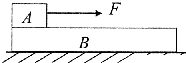
 如图,木块A放在木板B的左端,A、B间接触面粗糙,用恒力F将木块A拉到木板B的右端.第一次将B固定在水平地面上,第二次将B放在光滑水平地面上,则前后两个过程中相同的量是( )
如图,木块A放在木板B的左端,A、B间接触面粗糙,用恒力F将木块A拉到木板B的右端.第一次将B固定在水平地面上,第二次将B放在光滑水平地面上,则前后两个过程中相同的量是( )分析:分别对物块在两种情况下进行受力分析,求出加速度,根据运动学公式可求出时间,根据功的计算公式W=Fx可求力F对物块做的功,关键是公式中位移应是物块对地面的位移,不难分析当木板B不固定时物块对地面的位移大.
解答:解:A、不管木板B是否固定,木块A受到重力、支持力、拉力F和滑动摩擦力f,根据牛顿第二定律有F-f=ma,因f=μ
=μmg,可解得a=
,因此两种情况下的加速度相同,故A正确.
B、当木板固定时由x=
a
得t=
,当木板放在光滑的水平地面上时,由于A对B摩擦力作用,木板B将向右加速滑动,此时木块A滑动b右端时,A对地面的位移x=L+s,其中s是木板发生的位移,由x=
a
,可得
=
,故两种情况下木块A的运动时间不同.
C、根据W=Fx知,由于两种情况下木块A位移不同,故做的功不同.
D、根据“摩擦生热”公式Q=f
可知,两种情况下滑动摩擦力f相同,相对位移相同,所以系统产生的热量相同,故D正确.
故选AD.
| F | N |
| F-μmg |
| m |
B、当木板固定时由x=
| 1 |
| 2 |
| t | 2 |
|
| 1 |
| 2 |
| t | 2 |
| t | ′ |
|
C、根据W=Fx知,由于两种情况下木块A位移不同,故做的功不同.
D、根据“摩擦生热”公式Q=f
| S | 相对 |
故选AD.
点评:注意位移时间关系x=
t+
中的位移x应是对地面的位移,功的计算公式W=FL中的位移L也是对地面的位移.
| v | 0 |
| 1 |
| 2 |
| at | 2 |

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目