题目内容
19.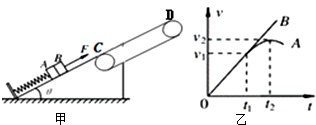 如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连.光滑斜面轨道与传送轨道良好对接,传送轨道平面与水平方向倾角也是θ,皮带传动装置顺时针匀速转动,物块B质量为m,初始时两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g.(t1和t2,v1和v2均未知)
如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连.光滑斜面轨道与传送轨道良好对接,传送轨道平面与水平方向倾角也是θ,皮带传动装置顺时针匀速转动,物块B质量为m,初始时两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图乙所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g.(t1和t2,v1和v2均未知)(1)求t2时刻弹簧的形变长度x.
(2)求t1的值.
(3)已知θ=37°,传送带两轮轴心相距L=5m,物体B与皮带间的动摩擦因数μ=0.25.设AB刚好在C点(斜面与传送带的连接点)分离并进入传送轨道,设物体B滑到传送带的C点时速度为8m/s,物体可视为质点,如果在物体B到达C点同时撤去拉力F,(sin37°=0.6,cos37°=0.8))若传送装置匀速转动的速度v可在v>4m/s的范围内调节,试推导物体B滑动到顶端D时速度vD随传送带速度v变化的关系式,g取l0m/s2.
分析 (1)A的速度最大时加速度为零,根据胡克定律求出A达到最大速度时的位移;
(2)由图读出,t1时刻A、B开始分离,对A根据牛顿第二定律和运动学公式求解t1;
(3)分传送带速度在4m/s<v<8m/s和v≥8m/s两个范围,根据运动学基本公式求解.
解答 解:(1)由图知,A的加速度为零,速度最大,根据牛顿第二定律和胡克定律得:
mgsinθ=kx,
得:$x=\frac{mgsinθ}{k}$
(2)由图读出,t1时刻A、B开始分离,对A根据牛顿第二定律:
kx-mgsinθ=ma
开始时有:2mgsinθ=kx0,又x0-x=$\frac{1}{2}a{{t}_{1}}^{2}$
联立以三式得:t1=$\sqrt{\frac{2(mgsinθ-ma)}{ak}}$.
(3)当传送带的速度在4m/s<v<8m/s的范围内调节时,物体B先以加速度a1减速向上滑行:${x_1}=\frac{{{v_0}^2-{v^2}}}{{2{a_1}}}$
当速度减到v后又以a2减速向上滑行,
物体B滑动到D点时速度vD随速度v的变化关系式是:${V_D}=\sqrt{\frac{V^2}{2}-8}$
当传送带的速度在v≥8m/s的范围内调节时,物体B将以加速度a2减速滑行到D点,
${V_D}^2-{V_0}^2=-2aL$
物体B滑动到D点时速度vD随速度v的变化关系式是:${V_D}=2\sqrt{6}m/s$
答:(1)t2时刻弹簧的形变长度x为$\frac{mgsinθ}{k}$.
(2)t1的值为$\sqrt{\frac{2(mgsinθ-ma)}{ak}}$.
(3)导物体B滑动到顶端D时速度vD随传送带速度v变化的关系式为:当4m/s<v<8m/s时${V}_{D}=\sqrt{\frac{{V}^{2}}{2}-8}$,当v≥8m/s时${V}_{D}=2\sqrt{6}m/s$.
点评 从受力角度看,两物体分离的条件是两物体间的正压力为0.从运动学角度看,一起运动的两物体恰好分离时,两物体在沿斜面方向上的加速度和速度仍相等.


| A. | 重力、竖直推力 | |
| B. | 重力、静摩擦力和竖直推力 | |
| C. | 竖直推力、静摩擦力 | |
| D. | 重力、墙壁对物体向左的弹力、竖直推力和静摩擦力 |
| A. | 研究运动员起跑动作时能够把他看做质点 | |
| B. | “物体在第5s内”指的物体在4s末到5s初这1s的时间 | |
| C. | 速度为零时加速度可能不为零,加速度增大时速度可能减小 | |
| D. | 单向直线运动中,物体的位移就是路程 |
| A. | 因为质点没有大小,所以与几何中的点没有区别 | |
| B. | 质点通过一段路程,位移可能是零 | |
| C. | 速度变化得越多,加速度就越大 | |
| D. | 加速度方向保持不变,速度方向也保持不变 |
| A. | 自由落体运动 | B. | 竖直下抛运动 | C. | 竖直上抛运动 | D. | 平抛运动 |

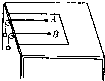 现在需要测量物块与长木板之间的动摩擦因数,备有如下器材:两个相同的物块A、B,两个带有固定装置的光滑小滑轮,卡子若干,一把镊子,一个黑板擦,几条长轻质细线,两个小盘.小丁和晓平两个同学配合进行如下实验:首先把木板固定在水平桌面上,把两小滑轮固定在木板的左端,把两个物块A和B(平行木板左边缘、AB距离较近)放到木板的右端,用细线把物块和小盘通过小滑轮连接,通过调整小滑轮的高度使木板上方的细线水平,在物块A和B右端固定好长细线;晓平同学用黑板擦按住两个物块A、B,小丁同学在两个小盘里放上不同个数的砝码,然后晓平同学抬起黑板擦,两个物块同时运动起来,当运动较快的物块接近木板左端时按下黑板擦,两个物块同时停下来.
现在需要测量物块与长木板之间的动摩擦因数,备有如下器材:两个相同的物块A、B,两个带有固定装置的光滑小滑轮,卡子若干,一把镊子,一个黑板擦,几条长轻质细线,两个小盘.小丁和晓平两个同学配合进行如下实验:首先把木板固定在水平桌面上,把两小滑轮固定在木板的左端,把两个物块A和B(平行木板左边缘、AB距离较近)放到木板的右端,用细线把物块和小盘通过小滑轮连接,通过调整小滑轮的高度使木板上方的细线水平,在物块A和B右端固定好长细线;晓平同学用黑板擦按住两个物块A、B,小丁同学在两个小盘里放上不同个数的砝码,然后晓平同学抬起黑板擦,两个物块同时运动起来,当运动较快的物块接近木板左端时按下黑板擦,两个物块同时停下来.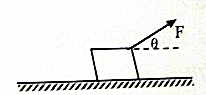 如图所示,用与水平成θ角的拉力F作用在物块上,物块沿水平面做匀速直线运动.已知地面的动摩擦因数为μ,物块的质量为m,求拉力的大小.
如图所示,用与水平成θ角的拉力F作用在物块上,物块沿水平面做匀速直线运动.已知地面的动摩擦因数为μ,物块的质量为m,求拉力的大小. 如图所示,三个电阻的阻值分别为R1=2R2=3R3,安培表的内阻忽略不计,则通过三个电阻的电流强度之比为1:2:3,两个安培表读数之比为5:3.
如图所示,三个电阻的阻值分别为R1=2R2=3R3,安培表的内阻忽略不计,则通过三个电阻的电流强度之比为1:2:3,两个安培表读数之比为5:3.