题目内容
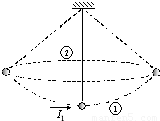
一轻绳一端连接一小球，另一端固定在悬点上．整个装置处于真空室内．开始时小球静止在最低点，一方向水平的冲量I1在极短时间内作用到小球上，使小球在竖直面内来回摆动，如图中①．此后，当小球某一次摆动到最高点时，又有另一方向水平的冲量I2在极短时间内作用到小球上，此后小球在水平面内做匀速圆周运动，如图中②，而且绳子的拉力大小与前面小球在摆动过程中绳子拉力的最大值相等．求冲量I1和冲量I2大小的比值
．
【答案】分析：摆动的小球在摆动过程中机械能守恒，则由机械能守恒可求得小球在最低点的速度，由牛顿第二定律可求得最低点时绳子的拉力表达式；
做圆周运动的小球重力的分力充当向心力，则可得出向心力的表达式，联立可求得冲量的比值．
解答：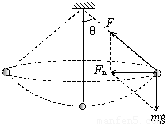
解：设小球质量为m，绳子长度为l，最大摆角为θ．在第一过程中I1=mv1①
小球摆动过程机械能守恒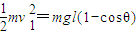
②
小球在最低点时绳子拉力最大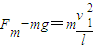
③
小球在水平面内做匀速圆周运动，小球速度大小为v2．I2=mv2④
设绳子拉力为F，则mg=Fcosθ⑤
小球的向心力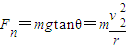
⑥
圆周半径r=lsinθ⑦
联立以上各式并将Fm=F代入可解得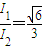
⑧
答：冲量I1和I2的比值为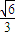
．
点评：本题将摆动和圆周运动结合在一起，注意摆动时机械能守恒，速度在发生变化；而匀速圆周运动，速度保持不变，合外力充当向心力．
做圆周运动的小球重力的分力充当向心力，则可得出向心力的表达式，联立可求得冲量的比值．
解答：
解：设小球质量为m，绳子长度为l，最大摆角为θ．在第一过程中I1=mv1①小球摆动过程机械能守恒
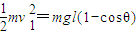②小球在最低点时绳子拉力最大
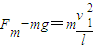③小球在水平面内做匀速圆周运动，小球速度大小为v2．I2=mv2④
设绳子拉力为F，则mg=Fcosθ⑤
小球的向心力
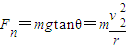⑥圆周半径r=lsinθ⑦
联立以上各式并将Fm=F代入可解得
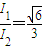⑧答：冲量I1和I2的比值为
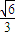．点评：本题将摆动和圆周运动结合在一起，注意摆动时机械能守恒，速度在发生变化；而匀速圆周运动，速度保持不变，合外力充当向心力．
练习册系列答案
中考解读考点精练系列答案
相关题目
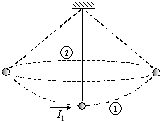一轻绳一端连接一小球，另一端固定在悬点上．整个装置处于真空室内．开始时小球静止在最低点，一方向水平的冲量I1在极短时间内作用到小球上，使小球在竖直面内来回摆动，如图中①．此后，当小球某一次摆动到最高点时，又有另一方向水平的冲量I2在极短时间内作用到小球上，此后小球在水平面内做匀速圆周运动，如图中②，而且绳子的拉力大小与前面小球在摆动过程中绳子拉力的最大值相等．求冲量I1和冲量I2大小的比值
．
kg的小球A，另一端挂在光滑水平轴O 上，O到小球的距离为L=0.1m，小球跟水平面接触，但无相互作用，在球的两侧等距离处分别固定一个光滑的斜面和一个挡板，如图所示，水平距离s=2m，动摩擦因数μ=0.25．现有一小滑块B，质量也为
，从斜面上滑下，每次与小球碰撞时相互交换速度，且与挡板碰撞不损失机械能．若不计空气阻力，并将滑块和小球都视为质点，g取10m/s2，（斜面底端与水平面光滑连接，即滑块通过连接点时无机械能损失）。试问：
处滑下与小球第一次碰撞后，使小球恰好在竖直平面内做完整的圆周运动，求此高度