题目内容
如图所示,电源电动势E=50V,内阻r=1Ω, R1=3Ω,R2=6Ω.间距d=0.2m的两平行金属板M、N水平放置,闭合开关S,板间电场视为匀强电场.板间竖直放置一根长也为d的光滑绝缘细杆AB,有一个穿过细杆的带电小球p,质量为m=0.01kg、带电量大小为q=1×10-3C(可视为点电荷,不影响电场的分布).现调节滑动变阻器R,使小球恰能静止在A处;然后再闭合K,待电场重新稳定后释放小球p.取重力加速度g=10m/s2.求:
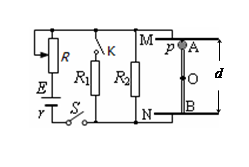
(1)小球的电性质和恰能静止时两极板间的电压;
(2)小球恰能静止时滑动变阻器接入电路的阻值;
(3)小球p到达杆的中点O时的速度.
略
解析:(1)(4分)小球带负电 (1分)
恰能静止应满足mg = Eq= Uq/d ( 2分)
U = mgd/q = 0.01×10×0.2/1×10-3 V= 20V ( 1分)
(2)(3分)小球恰能静止时滑动变阻器接入电路的阻值为Rx,由电路电压关系:
E/(Rx+R2+r) =U/R2 ( 2分)
代入数据求得Rx =8Ω ( 1分)
(3)(6分)闭合电键K后,设电场稳定时的电压为U/,
由电路电压关系:E/(Rx+R12+r) =U//R12
代入数据求得U/ = 100/11V (3分)
由动能定理:mgd/2 - U/q/2 =mv2/2 ( 2分)
代入数据求得v = 1.05m/s ( 1分)

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
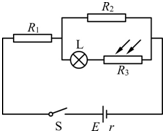 如图所示,电源电动势为E,内电阻为r,L为小灯泡(其灯丝电阻可视为不变),R1和R2为定值电阻,R3为光敏电阻,其阻值的大小随照射光强度的增强而减小.闭合开关S后,将照射光强度增强,则( )
如图所示,电源电动势为E,内电阻为r,L为小灯泡(其灯丝电阻可视为不变),R1和R2为定值电阻,R3为光敏电阻,其阻值的大小随照射光强度的增强而减小.闭合开关S后,将照射光强度增强,则( )| A、电路的路端电压将增大 | B、灯泡L将变暗 | C、R1两端的电压将增大 | D、内阻r上发热的功率将增大 |
 如图所示,电源电动势为E,内电阻为r,当滑动变阻器的触片P从右端滑到左端时,发现电压表V1、V2示数为U1、U2,示数变化的绝对值分别为△U1和△U2,电流表的示数为I,电流表示数变化的绝对值为△I,下列说法中正确的是( )
如图所示,电源电动势为E,内电阻为r,当滑动变阻器的触片P从右端滑到左端时,发现电压表V1、V2示数为U1、U2,示数变化的绝对值分别为△U1和△U2,电流表的示数为I,电流表示数变化的绝对值为△I,下列说法中正确的是( )| A、小灯泡L1、L2变暗,L3变亮 | ||||
| B、小灯泡L3变暗,L1、L2变亮 | ||||
| C、△U1<△U2 | ||||
D、
|
 (2011?静安区一模)如图所示,电源电动势E=50V,内阻r=1Ω,R1=30Ω,R2=60Ω.间距d=0.2m的两平行金属板M、N水平放置,闭合开关S,板间电场视为匀强电场.板间竖直放置一根长也为d的光滑绝缘细杆AB,有一个穿过细杆的带电小球p,质量为m=1×10-2kg、电荷量为q=+1×10-3C(可视为点电荷,不影响电场的分布),现将小球p从杆的顶端A处由静止释放,小球p沿杆向下运动到杆的中点O时,速度为v=2m/s.求:
(2011?静安区一模)如图所示,电源电动势E=50V,内阻r=1Ω,R1=30Ω,R2=60Ω.间距d=0.2m的两平行金属板M、N水平放置,闭合开关S,板间电场视为匀强电场.板间竖直放置一根长也为d的光滑绝缘细杆AB,有一个穿过细杆的带电小球p,质量为m=1×10-2kg、电荷量为q=+1×10-3C(可视为点电荷,不影响电场的分布),现将小球p从杆的顶端A处由静止释放,小球p沿杆向下运动到杆的中点O时,速度为v=2m/s.求: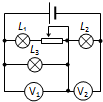 如图所示,电源电动势为E,内电阻为r.当滑动变阻器的触片P从右端滑到左端时,发现电压表V1、V2示数变化的绝对值分别为△U1和△U2,下列说法中正确的是( )
如图所示,电源电动势为E,内电阻为r.当滑动变阻器的触片P从右端滑到左端时,发现电压表V1、V2示数变化的绝对值分别为△U1和△U2,下列说法中正确的是( )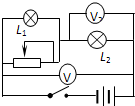 如图所示,电源电动势为E,内电阻为r.两电压表可看作是理想电表,当闭合开关,将滑动变阻器的触片由右端向左滑动时,下列说法中正确的是( )
如图所示,电源电动势为E,内电阻为r.两电压表可看作是理想电表,当闭合开关,将滑动变阻器的触片由右端向左滑动时,下列说法中正确的是( )