题目内容
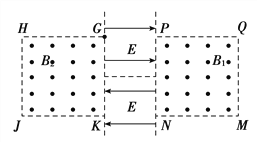
【题目】如图所示，某空间中有四个方向垂直于纸面向里、磁感应强度大小相同、半径均为R的圆形匀强磁场区域1、2、3、4。其中1与4相切，2相切于1和3,3相切于2和4，且第1个磁场区域和第4个磁场区域的竖直方向的直径在一条直线上。一质量为m、带电荷量为－q的粒子，静止置于电势差为U0的带电平行板(竖直放置)形成的电场中(初始位置在负极板附近)，经过电场加速后，从第1个磁场的最左端水平进入，并从第3个磁场的最下端竖直穿出。已知tan 22.5°=0.4，不计带电粒子的重力。
（1）求带电粒子进入磁场时的速度大小；
（2）试判断：若在第3个磁场的下面也有一电势差为U0的带电平行板(水平放置，其小孔在第3个磁场最下端的正下方)形成的电场，带电粒子能否按原路返回？请说明原因；
（3）求匀强磁场的磁感应强度大小B；
（4）若将该带电粒子自该磁场中的某个位置以某个速度释放后恰好可在四个磁场中做匀速圆周运动，则该粒子的速度大小v′为多少？
【答案】（1）
（2）见解析（3）
（4）
【解析】(1)根据动能定理有： 
，解得
(2)不能按原路返回，因为粒子进入第3个磁场下的电场后，向下减速至速度为零，然后反向加速至速度的大小为v，但进入磁场后，根据左手定则可知，带电粒子受到的洛伦兹力方向向右，粒子向右偏，故不能按原路返回
(3)设带电粒子在磁场中做圆周运动的半径为r，如图甲所示
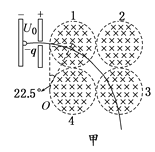
则根据运动的对称性和几何关系可知，粒子在第1个磁场和第3个磁场中各偏转45°，则有： 
，解得r＝2.5R
根据洛伦兹力提供向心力得
解得
(4)该带电粒子在四个磁场中做匀速圆周运动，如图乙所示
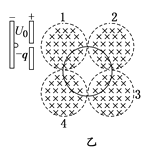
由几何关系知其轨道半径只能是R，根据洛伦兹力提供向心力得
解得
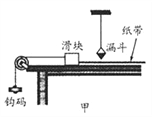
【题目】某同学利用如图甲所示的气垫导轨装置探究恒力做功与物体动能变化间的关系．在气垫导轨上安装了光电门，滑块上固定宽度为d的遮光条，用细线绕过定滑轮将质量为M＝200 g的滑块(含遮光条)与质量为m＝30 g的重物相连，细线与导轨平行．实验时滑块每次都从同一位置A处由静止释放，用x表示滑块从静止开始到通过光电门的位移大小，用t表示遮光条通过光电门的时间．改变光电门在气垫导轨上的位置，测量不同x所对应遮光条通过光电门的时间t，再分别计算拉力做的功W和滑块通过光电门时的动能Ek.
(1) 用游标卡尺测量遮光条的宽度d，示数如图乙所示，则d＝________cm.
(2) 实验前调节气垫导轨水平的目的是________________________________________．
(3) 将重物的重力视为滑块受到的拉力，取g＝9.80 m/s2，用W＝mgx计算出拉力对滑块做的功W，并计算出滑块动能增量ΔEk.计算结果见下表：
W/10－3 J | 7.35 | 8.82 | 10.29 | 11.76 | 13.23 | 14.70 |
ΔEk/10－3 J | 6.39 | 7.67 | 8.95 | 10.23 | 11.50 | 12.78 |
(W－ΔEk)/10－3 J | 0.96 | 1.15 | 1.34 | 1.53 | 1.73 | 1.92 |
①实验结果表明，ΔEk总是小于W.你认为这是________(选填“偶然”或“系统”)误差，简要说明你的理由：__________________________________________________________.
②进一步研究表明，拉力对小车做的功W和小车动能增量ΔEk的差值(W－ΔEk)随x增大而增大，用题中滑块和重物的质量可计算出(W－ΔEk)与x的比值
＝________．(计算结果保留两位有效数字)
