题目内容
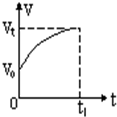 如图所示为一物体做直线运动的V-t图象,初速度为V0,末速度为Vt,则物体在时间t1内的平均速度为( )
如图所示为一物体做直线运动的V-t图象,初速度为V0,末速度为Vt,则物体在时间t1内的平均速度为( )分析:本题考查速度图象与时间轴围成的面积等于物体通过的位移,根据x=
t可得物体的平均速度;匀变速直线运动的平均速度等于初末速度的算术平均值,连接初末两点,即可得到匀变速直线运动的速度图象,从而得到实际运动的位移和匀变速直线运动的位移的大小关系,从而得到他们的平均速度的大小关系.
. |
| v |
解答:解:如图连接初末两时刻的速度图象如虚线所示,则物体做匀加速直线运动,则匀加速运动的平均速度
=
,物体通过的位移x1=
t,位移为梯形面积.
而物体实际运动的速度图象如实线所示,物体通过的位移为整个图象与时间轴围成的面积x,则x=
t,显然x>x1,故
>
,故B正确.
故选B.
. |
| v1 |
| v0+vt |
| 2 |
| v0+vt |
| 2 |
而物体实际运动的速度图象如实线所示,物体通过的位移为整个图象与时间轴围成的面积x,则x=
. |
| v |
. |
| v |
| v0+vt |
| 2 |
故选B.

点评:解决此题的关键是:速度图象与时间轴围成的面积等于物体通过的位移,匀变速直线运动的平均速度等于初末速度的算术平均值.

练习册系列答案
相关题目
 本题有①、②两个小题,每位考生只需自主选做其中一个小题.
本题有①、②两个小题,每位考生只需自主选做其中一个小题.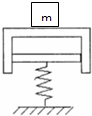 如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止,气缸和活塞的总质量为M,气缸内封闭一定质量的理想气体.设活塞和缸壁间无摩擦且可以在缸内自由移动,缸壁导热性能良好,不漏气,外界大气的压强和温度不变.现在气缸顶上缓慢放上一个质量为m的物体.当系统平衡时,下列说法正确的是( )
如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止,气缸和活塞的总质量为M,气缸内封闭一定质量的理想气体.设活塞和缸壁间无摩擦且可以在缸内自由移动,缸壁导热性能良好,不漏气,外界大气的压强和温度不变.现在气缸顶上缓慢放上一个质量为m的物体.当系统平衡时,下列说法正确的是( ) (2007?居巢区模拟)如图所示为一物体在空气中做竖直上抛运动的上升阶段的v-t图象,试由图象判断:该物体的初速度多大?最大上升高度是多少?是否受空气阻力,如果受到空气阻力,空气阻力大小是否恒定,并加以说明?定性画出下降阶段的v-t图线.
(2007?居巢区模拟)如图所示为一物体在空气中做竖直上抛运动的上升阶段的v-t图象,试由图象判断:该物体的初速度多大?最大上升高度是多少?是否受空气阻力,如果受到空气阻力,空气阻力大小是否恒定,并加以说明?定性画出下降阶段的v-t图线.