Question

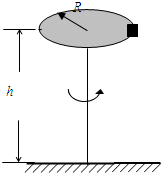如图所示，一水平圆盘绕过圆心的竖直轴匀速转动，圆盘边缘有一个小物块．当圆盘转动的角速度达到某一数值，再增大时，物块从圆盘边缘滑落到地面．已知圆盘半径R=0.5m，物块与圆盘间的动摩擦因数为μ=0.2，最大静摩擦力等于滑动摩擦力，圆盘中心与地面的距离为h=10m，g=10m/s²．求：（1）圆盘转动时能保证物块相对圆盘静止的最大角速度．（2）物块落地点到圆盘中心的水平距离为多大？

Answer 1

分析：（1）由最大静摩擦力提供向心力，结合向心力公式即可求解；
（2）滑块离开圆盘后做平抛运动，根据平抛运动的基本公式即可求解．

解答：解：（1）设圆盘的角速度为ω时，滑块从圆盘上滑落，此时，f_max=μmg
μmg=mRω²
ω=2rad/s
（2）滑块离开圆盘后做平抛运动，v=ωR=1m/s
设水平位移为x，由平抛运动规律得：x=vt
h=

1

2

gt2
∴x=

2

m
由空间几何关系得
s=

R2+x2

=1.5m
答：（1）圆盘转动时能保证物块相对圆盘静止的最大角速度为2rad/s．
（2）物块落地点到圆盘中心的水平距离为1.5m

点评：本题主要考查了向心力公式及平抛运动基本公式的直接应用，并能结合几何关系求解，难度适中．