题目内容
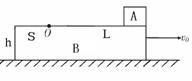 如图所示,粗糙水平地面上有一高为h=0.2m的木板B,B的上表面以O点为界,O点以右是光滑的,O点以左是粗糙的。O点离B最右端距离为L=1.25m、离B左端的距离S=0.32m 。现在B的最右端放一个可看成质点的、质量与B相同的木块A,A、B均处于静止。已知B与地之间的动摩擦因数为μ1=0.1,A、B之间动摩擦因数为μ2=0.2,A、B质量均为m。现给B一个水平向右的瞬时冲量,使B获得初速度v0=3m/s,求:
如图所示,粗糙水平地面上有一高为h=0.2m的木板B,B的上表面以O点为界,O点以右是光滑的,O点以左是粗糙的。O点离B最右端距离为L=1.25m、离B左端的距离S=0.32m 。现在B的最右端放一个可看成质点的、质量与B相同的木块A,A、B均处于静止。已知B与地之间的动摩擦因数为μ1=0.1,A、B之间动摩擦因数为μ2=0.2,A、B质量均为m。现给B一个水平向右的瞬时冲量,使B获得初速度v0=3m/s,求:
(1)当B向右运动1.25m时,A、B的速度大小。
(2)若B向右运动1.25m时,B突然受到一个向右的水平拉力F=0.2mg,则此拉力作用0.4s 时,A木块离O点的水平距离是多少?。
(1)0;2m/s (2)0.58m
解析:
(1)A保持静止,vB=2m/s (2)ΔS=0.58m
(1)在B向右运动1.25m这一过程中,因A受的合外力为零,则A保持静止,即 vA0=0.
设此时 B的速度大小为![]()
对B由动能定理 得 2 ![]()
解①得 vB=2m/s
(2)这时A加速、B减速,设A、B最后达到的共同速度为![]() ,
,
在这一过程A在B上滑行的距离为s0
则由动量守恒定律 得 ![]()
由能量守恒定律 得
![]() mgs0=
mgs0=![]()
解②③得 S0=0.5m
由于![]() ,可知: A将从B上表面滑落。设A刚好滑离B时A、B的速度分别为
,可知: A将从B上表面滑落。设A刚好滑离B时A、B的速度分别为![]() 、
、![]() ,设A在B上自O点至滑落所用时间为
,设A在B上自O点至滑落所用时间为![]() ,
,
由动量守恒定律 得 mvB=mvA+m![]()
由能量守恒定律 得
![]()
解④⑤得 vA=0.4m/s ![]() =1.6m/s
=1.6m/s
对A由动量定理 得 ![]()
由⑥得t1=0.2s
A从B上滑落后以vA的初速度向右作平抛运动
设A经时间t2落地,t2内A的水平位移为x
h=![]()
x=vA t2
解⑦⑧得 t2=0.2s,![]() =0.08m.
=0.08m.
A作平抛运动的同时, B向右作加速运动,设其加速度为![]()
由牛顿第二定律 得 ![]()
设t2内B运动的距离为![]()
![]()
故B受F作用0.4s时A离O点的水平距离ΔS为:
ΔS=![]() +
+![]() -
-![]()
解⑨⑩(11)得 ΔS=0.58m。

 滑块C离开A时的速度VC’
滑块C离开A时的速度VC’