题目内容
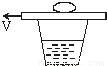
 如图所示,静止放在水平光滑的桌面上的纸带,其上有一质量为m=1.0kg的铁块,它与纸带右端的距离为L=0.5m,铁块与纸带间的动摩擦因数为μ=0.1.现用力F水平向左将纸带从铁块下抽出,当纸带全部抽出时铁块恰好到达桌面边缘,铁块抛出后落地点离抛出点的水平距离为x=0.8m.已知g=10m/s2,桌面高度为H=0.8m,不计纸带质量,不计铁块
如图所示,静止放在水平光滑的桌面上的纸带,其上有一质量为m=1.0kg的铁块,它与纸带右端的距离为L=0.5m,铁块与纸带间的动摩擦因数为μ=0.1.现用力F水平向左将纸带从铁块下抽出,当纸带全部抽出时铁块恰好到达桌面边缘,铁块抛出后落地点离抛出点的水平距离为x=0.8m.已知g=10m/s2,桌面高度为H=0.8m,不计纸带质量,不计铁块
大小,铁块不翻滚.求:
(1)铁块抛出时速度大小;
(2)纸带从铁块下抽出所用时间.
解:(1)设铁块抛出时的初速度为v0,由平抛运动规律,有
水平方向:x=v0t
竖直方向:H= gt2解得
gt2解得
v0=2m/s
(2)纸带从铁块下抽出所用的时间与铁块向左运动到桌边的时间相等.
开始时距离桌面左端的距离就等于铁块在桌面上向左运动的位移.
铁块向左运动过程中,a= =μg=1m/s2
=μg=1m/s2
由公式v0=at
则有纸带抽出后铁块的速度可得:t=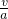 =
=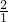 s=2s,
s=2s,
即得t=2s
答:(1)铁块抛出时速度大小2m/s;
(2)纸带从铁块下抽出所用的时间2s.
分析:(1)铁块离开桌面后做平抛运动,根据分位移公式列式求解得到初速度;
(2)对铁块受力分析,根据牛顿第二定律求出加速度,然后根据位移公式求得铁块直线加速的时间.
点评:本题关键是先分析清楚物体的运动情况,然后运用平抛运动的分位移公式、牛顿运动定律和运动学公式联立列式求解.
水平方向:x=v0t
竖直方向:H=
 gt2解得
gt2解得v0=2m/s
(2)纸带从铁块下抽出所用的时间与铁块向左运动到桌边的时间相等.
开始时距离桌面左端的距离就等于铁块在桌面上向左运动的位移.
铁块向左运动过程中,a=
 =μg=1m/s2
=μg=1m/s2由公式v0=at
则有纸带抽出后铁块的速度可得:t=
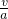 =
=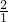 s=2s,
s=2s,即得t=2s
答:(1)铁块抛出时速度大小2m/s;
(2)纸带从铁块下抽出所用的时间2s.
分析:(1)铁块离开桌面后做平抛运动,根据分位移公式列式求解得到初速度;
(2)对铁块受力分析,根据牛顿第二定律求出加速度,然后根据位移公式求得铁块直线加速的时间.
点评:本题关键是先分析清楚物体的运动情况,然后运用平抛运动的分位移公式、牛顿运动定律和运动学公式联立列式求解.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
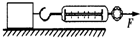
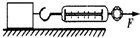
 在研究摩擦力的实验中,如图所示,用弹簧秤水平拉一放在水平桌面上的小木块,小木块的运动状态及弹簧秤的读数如表格所示(每次实验时,木块与桌面的接触面相同).则由表分析可知( ) 在研究摩擦力的实验中,如图所示,用弹簧秤水平拉一放在水平桌面上的小木块,小木块的运动状态及弹簧秤的读数如表格所示(每次实验时,木块与桌面的接触面相同).则由表分析可知( )
|
在研究摩擦力的实验中,如图所示,用弹簧秤水平拉一放在水平桌面上的小木块,小木块的运动状态及弹簧秤的读数如表格所示(每次实验时,木块与桌面的接触面相同).则由表分析可知( )
A.木块受到的最大静摩擦力为0.7N
B.木块受到的最大静摩擦力可能为0.6N
C.在这五次实验中,木块受到的摩擦力大小有三次是相同的
D.在这五次实验中,木块受到的摩擦力大小只有两次是相同的
| 实验次数 | 运动状态 | 弹簧秤读数/N |
| 1 | 静止 | 0.4 |
| 2 | 静止 | 0.6 |
| 3 | 加速 | 0.7 |
| 4 | 匀速 | 0.5 |
| 5 | 减速 | 0.3 |

A.木块受到的最大静摩擦力为0.7N
B.木块受到的最大静摩擦力可能为0.6N
C.在这五次实验中,木块受到的摩擦力大小有三次是相同的
D.在这五次实验中,木块受到的摩擦力大小只有两次是相同的
在研究摩擦力的实验中,如图所示,用弹簧秤水平拉一放在水平桌面上的小木块,小木块的运动状态及弹簧秤的读数如表格所示(每次实验时,木块与桌面的接触面相同).则由表分析可知( )
A.木块受到的最大静摩擦力为0.7N
B.木块受到的最大静摩擦力可能为0.6N
C.在这五次实验中,木块受到的摩擦力大小有三次是相同的
D.在这五次实验中,木块受到的摩擦力大小只有两次是相同的
| 实验次数 | 运动状态 | 弹簧秤读数/N |
| 1 | 静止 | 0.4 |
| 2 | 静止 | 0.6 |
| 3 | 加速 | 0.7 |
| 4 | 匀速 | 0.5 |
| 5 | 减速 | 0.3 |

A.木块受到的最大静摩擦力为0.7N
B.木块受到的最大静摩擦力可能为0.6N
C.在这五次实验中,木块受到的摩擦力大小有三次是相同的
D.在这五次实验中,木块受到的摩擦力大小只有两次是相同的
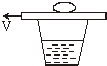 如图所示,装有适量水的玻璃杯口放上硬纸片,现将鸡蛋放在硬纸片上,用手指突然弹击硬纸片,产生的结果是( )
如图所示,装有适量水的玻璃杯口放上硬纸片,现将鸡蛋放在硬纸片上,用手指突然弹击硬纸片,产生的结果是( )