题目内容
如图所示的皮带传动装置中，右边两轮粘在一起且同轴，A、B、C三点均是各轮边缘上的一点，半径RA=RC=2RB，皮带不打滑，则：线速度vA：vB：vC=1：1：2
1：1：2
；向心加速度aA：aB：aC=1：2：4
1：2：4
．分析：（1）由v=ωr知线速度相同时，角速度与半径成反比；角速度相同时，线速度与半径成正比．
（2）由a=ωv结合角速度和线速度的比例关系，可以知道加速度的比例关系．
（2）由a=ωv结合角速度和线速度的比例关系，可以知道加速度的比例关系．
解答：解：因为A、B两轮由不打滑的皮带相连，所以相等时间内A、B两点转过的弧长相等，即vA=vB．
由v=ωr知；
=
=
又B、C是同轴转动，相等时间转过的角度相等，即ωB=ωA，
由v=ωr知，
=
=
所以：vA：vB：vC=1：1：2，
再根据a=ωv得 aA：aB：aC=1：2：4
故答案为：1：1：2，1：2：4
由v=ωr知；
| ωA |
| ωB |
| RB |
| RA |
| 1 |
| 2 |
又B、C是同轴转动，相等时间转过的角度相等，即ωB=ωA，
由v=ωr知，
| vB |
| vC |
| rB |
| rC |
| 1 |
| 2 |
所以：vA：vB：vC=1：1：2，
再根据a=ωv得 aA：aB：aC=1：2：4
故答案为：1：1：2，1：2：4
点评：题目主要考查v=ωr及a=ωv的应用，并注意各自半径的关系，属于简单题目．
练习册系列答案
相关题目
（2012?徐汇区一模）如图所示的皮带传动装置中，A、B两轮半径分别为rA和rB，已知rA＜rB，且皮带不打滑．在传动过程中，下列说法正确的是（ ）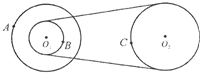
如图所示的皮带传动装置中，轮A和B同轴，A、B、C分别是三个轮边缘的质点，且RA=RC=2RB岛，若传动过程中皮带不打滑，则下列说法正确的是（ ）
（2006?济南模拟）如图所示的皮带传动装置中，轮B和C同轴，A、B、C分别是三个轮边缘的质点，且其半径RA=RC=2RB，则三质点的向心加速度之比aA：aB：aC等于（ ）
如图所示的皮带传动装置中，图中A、B、C三点的半径关系为RA=2RB=2RC，设皮带不打滑，则有VA：VB：VC=
如图所示的皮带传动装置中，轮A和B同轴，A、B、C分别是三个轮边缘的质点，且RA=RC=3RB，则三质点的向心加速度之比aA：aB：aC等于（ ）| A、9：3：1 | B、3：1：3 | C、1：3：9 | D、9：1：9 |