题目内容
【题目】如图所示，倾角为37°的斜面体靠在固定的竖直挡板P的一侧，一根轻绳跨过固定在斜面顶端的定滑轮，绳的一端与质量为mA=3kg的物块A连接，另一端与质量为mB=1kg的物块B连接。开始时使A静止于斜面上，B悬空。现释放物块A，物块A将在斜面上沿斜面匀加速下滑，求此过程中挡板P对斜面体的作用力的大小。（所有接触面产生的摩擦均忽略不计，sin37°=0.6 ，cos37°=0.8，g=10m/s2）
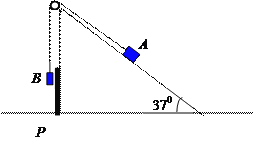
【答案】解：设绳中张力为T，斜面对A的支持你为NA，A、B加速度大小为a，以A为研究对象，由牛顿第二定律
mAgsin37° －T=ma①
NA=mAgcos37°④ ②
以B为研究对象，由牛顿第二定律
T－mBg=mBa③
联立解得a= 2m/s2T=" 12N "NA= 24N
以斜面体为研究对象，受力分析后，在水平方向
F=N′Asin37°－Tcos37° ④
NA=N′A
解得F= 4．8N
（或以整体为研究对象，由牛顿第二定律得F=mAacos37°）=4．8N）
【解析】略
练习册系列答案
相关题目
