题目内容
如图所示,劲度系数为k的弹簧下悬挂一个质量为m的重物,处于静止状态.手托重物使之缓慢上移,直到弹簧恢复原长,然后放手使重物从静止开始下落,重物下落过程中的最大速度为v,不计空气阻力.下列说法正确的是( )


A.手对重物做的功W1=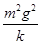 |
B.重物从静止下落到速度最大过程中重物克服弹簧弹力所做的功W2=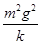 - -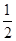 mv2 mv2 |
| C.弹性势能最大时小球加速度大小为g |
D.最大的弹性势能为 |
BCD
试题分析:质量为m的重物,处于静止状态,弹簧的型变量
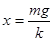 ,开始时手对重物的作用力大小为mg,其后逐渐减小,所以手对重物做的功小于
,开始时手对重物的作用力大小为mg,其后逐渐减小,所以手对重物做的功小于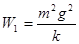 ,A错。重物从静止下落到速度最大过程中重物克服弹簧所做的功为
,A错。重物从静止下落到速度最大过程中重物克服弹簧所做的功为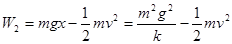 ,B对。弹性势能最大时小球速度为零重力势能全部转化为弹性势能(
,B对。弹性势能最大时小球速度为零重力势能全部转化为弹性势能(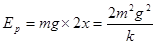 ),D对,根据对称性知道加速度跟初始时加速度大小相等方向相反,即加速度大小为g,C对。故选BCD
),D对,根据对称性知道加速度跟初始时加速度大小相等方向相反,即加速度大小为g,C对。故选BCD点评:本题难度较大,退与弹力做功,由于弹力为变力,因此W=Fs公式不再适用,应利用动能定理求解,克服弹簧弹力做了多少功,弹性势能就增大多少

练习册系列答案
相关题目



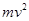
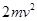

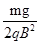
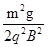
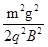
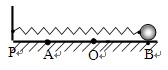

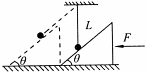
 的静止三角形物块刚好接触.现在用水平力F向左非常缓慢的推动三角形物块,直至轻绳与斜面平行,不计一切摩擦.关于该过程中,下列说法中正确的是( )
的静止三角形物块刚好接触.现在用水平力F向左非常缓慢的推动三角形物块,直至轻绳与斜面平行,不计一切摩擦.关于该过程中,下列说法中正确的是( )