题目内容
15.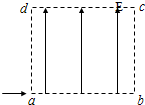 如图所示,矩形区域abcd内存在着匀强电场,ab=cd=L,ad=bc=$\frac{{\sqrt{3}}}{2}L$.电量为q、质量为m、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.若粒子从c点离开电场,求:
如图所示,矩形区域abcd内存在着匀强电场,ab=cd=L,ad=bc=$\frac{{\sqrt{3}}}{2}L$.电量为q、质量为m、动能为Ek的带电粒子从a点沿ab方向进入电场,不计重力.若粒子从c点离开电场,求:(1)带电粒子从c点离开电场时速度的大小及速度与cd的夹角;
(2)匀强电场的电场强度.
分析 (1)将带电粒子的运动沿着水平和竖直方向正交分解,运用分位移公式列式求带电粒子从c点离开电场时速度的大小,并确定速度的方向.
(2)由动能定理列式求解场强.
解答 解:(1)粒子的初动能为:EK=$\frac{1}{2}$mv02
则 v0=$\sqrt{\frac{2{E}_{k}}{m}}$
粒子在ab方向上作匀速直线运动,有:L=v0t
粒子在ad方向上做初速度为0的匀加速直线运动,有:$\frac{{\sqrt{3}}}{2}L$=$\frac{{v}_{y}}{2}t$
带电粒子从c点离开电场时速度的大小为:v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$
联立解得:v=2v0=2$\sqrt{\frac{2{E}_{k}}{m}}$
设速度与cd的夹角为α.则tanα=$\frac{{v}_{y}}{{v}_{0}}$=$\sqrt{3}$,α=60°
(2)根据动能定理得:
qE•$\frac{{\sqrt{3}}}{2}L$=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得 E=$\frac{8\sqrt{3}{E}_{k}}{3qL}$
答:(1)带电粒子从c点离开电场时速度的大小是2$\sqrt{\frac{2{E}_{k}}{m}}$,速度与cd的夹角是60°;
(2)匀强电场的电场强度$\frac{8\sqrt{3}{E}_{k}}{3qL}$.
点评 本题关键将带电粒子的运动沿初速度方向和电场方向进行正交分解,然后根据运动学公式和动能定理列式求解.

练习册系列答案
相关题目
5.下列关于匀速圆周运动的说法正确的是( )
| A. | 物体做圆周运动而产生一个向心力 | |
| B. | 向心力始终指向圆心,所以向心力是恒定的 | |
| C. | 向心加速度只改变线速度的大小 | |
| D. | 向心加速度只改变线速度的方向 |
6. 2010年4月17日是青海玉树震后第三天,中国空军日以继夜加紧进行空运抗震救灾,当天上午6时至10时又出动飞机4个架次,向玉树地震灾区运送帐篷540顶(约合57吨),野战食品24吨.从水平匀速飞行的运输机上向外自由释放一个物体如图,不计空气阻力,在物体下落过程中,下列说法正确的是( )
2010年4月17日是青海玉树震后第三天,中国空军日以继夜加紧进行空运抗震救灾,当天上午6时至10时又出动飞机4个架次,向玉树地震灾区运送帐篷540顶(约合57吨),野战食品24吨.从水平匀速飞行的运输机上向外自由释放一个物体如图,不计空气阻力,在物体下落过程中,下列说法正确的是( )
 2010年4月17日是青海玉树震后第三天,中国空军日以继夜加紧进行空运抗震救灾,当天上午6时至10时又出动飞机4个架次,向玉树地震灾区运送帐篷540顶(约合57吨),野战食品24吨.从水平匀速飞行的运输机上向外自由释放一个物体如图,不计空气阻力,在物体下落过程中,下列说法正确的是( )
2010年4月17日是青海玉树震后第三天,中国空军日以继夜加紧进行空运抗震救灾,当天上午6时至10时又出动飞机4个架次,向玉树地震灾区运送帐篷540顶(约合57吨),野战食品24吨.从水平匀速飞行的运输机上向外自由释放一个物体如图,不计空气阻力,在物体下落过程中,下列说法正确的是( )| A. | 从飞机上看,物体静止 | |
| B. | 从飞机上看,物体始终在飞机的后方 | |
| C. | 从地面上看,物体做平抛运动 | |
| D. | 从地面上看,物体做自由落体运动 |
3.考汽车驾照时需要进行路考,路考中有一项是定点停车.在一次定点停车考试中,某学员驾驶汽车以8m/s的速度匀速行驶,当车头与路旁竖立的标志杆相距20m时,学员立即刹车,让车做匀减速直线运动,结果车头恰好停在标志杆处,忽略学员的反应时间,下列说法正确的是( )
| A. | 汽车刹车过程的加速度大小为0.8m/s2 | |
| B. | 汽车刹车过程的加速度大小为1.2m/s2 | |
| C. | 汽车刹车过程的时间为2.5s | |
| D. | 汽车刹车过程的时间为5s |
4. 如图所示,用绝缘细线拴一个带负电的小球,让它在竖直向下的匀强电场中绕O点做竖直平面内的圆周运动,a、b两点分别是圆周的最高点和最低点,则( )
如图所示,用绝缘细线拴一个带负电的小球,让它在竖直向下的匀强电场中绕O点做竖直平面内的圆周运动,a、b两点分别是圆周的最高点和最低点,则( )
 如图所示,用绝缘细线拴一个带负电的小球,让它在竖直向下的匀强电场中绕O点做竖直平面内的圆周运动,a、b两点分别是圆周的最高点和最低点,则( )
如图所示,用绝缘细线拴一个带负电的小球,让它在竖直向下的匀强电场中绕O点做竖直平面内的圆周运动,a、b两点分别是圆周的最高点和最低点,则( )| A. | 小球经过a点时,线中的张力最大 | B. | 小球经过b点时,电势能最小 | ||
| C. | 小球经过a点时,电势能最小 | D. | 小球经过b点时,机械能最小 |
5. 如图所示,L是自感系数很大的线圈,其电阻几乎为零.A和B是两个完全相同的灯泡,下列说法中正确的是( )
如图所示,L是自感系数很大的线圈,其电阻几乎为零.A和B是两个完全相同的灯泡,下列说法中正确的是( )
 如图所示,L是自感系数很大的线圈,其电阻几乎为零.A和B是两个完全相同的灯泡,下列说法中正确的是( )
如图所示,L是自感系数很大的线圈,其电阻几乎为零.A和B是两个完全相同的灯泡,下列说法中正确的是( )| A. | 当开关S闭合瞬间,A灯先亮B灯后亮 | |
| B. | 当开关S闭合瞬间,A灯比B灯亮 | |
| C. | 当开关S断开瞬间,流经灯泡B的电流是由b到a | |
| D. | 当开关S断开瞬间,流经灯泡B的电流是由a到b |
 2004年7月25日,中国用长征运载火箭成功地发射了“探测2号”卫星.右图是某监测系统每隔2.5s拍摄的关于起始匀加速阶段火箭的一组照片.已知火箭的长度为40m,用刻度尺测量照片上的长度,结果如图所示.
2004年7月25日,中国用长征运载火箭成功地发射了“探测2号”卫星.右图是某监测系统每隔2.5s拍摄的关于起始匀加速阶段火箭的一组照片.已知火箭的长度为40m,用刻度尺测量照片上的长度,结果如图所示. 如图所示的电路中,R1=R3=10Ω,当电键K闭合时,电压表和电流表的示数分别是6V和0.2A,当电键K断开时,电压表的示数变为4.4V,求:
如图所示的电路中,R1=R3=10Ω,当电键K闭合时,电压表和电流表的示数分别是6V和0.2A,当电键K断开时,电压表的示数变为4.4V,求: