题目内容
【题目】粒子回旋加速器的工作原理如图所示,置于真空中的D形金属盒的半径为R,两金属盒间的狭缝很小,磁感应强度为B的匀强磁场与金属盒盒面垂直,高频交流电的频率为f,加速电压为U,若中心粒子源处产生的质子质量为m、电荷量为+e,在加速器中被加速.不考虑相对论效应,则下列说法正确的是( )
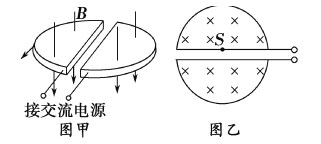
A. 不改变磁感应强度B和交流电的频率f,该加速器也可加速α粒子
B. 加速的粒子获得的最大动能随加速电压U的增大而增大
C. 质子被加速后的最大速度不能超过2πRf
D. 质子第二次和第一次经过D形盒间狭缝后轨道半径之比为 ![]() ∶1
∶1
【答案】CD
【解析】回旋加速器运用电场加速磁场偏转来加速粒子,根据洛伦兹力提供向心力可以求出粒子的最大速度,从而求出最大动能.在加速粒子的过程中,电场的变化周期与粒子在磁场中运动的周期相等.
解:A、带电粒子在磁场中运动的周期与加速电场的周期相等,根据T=![]() 知,换用α粒子,粒子的比荷变化,周期变化,回旋加速器需改变交流电的频率才能加速α粒子.故A错误.
知,换用α粒子,粒子的比荷变化,周期变化,回旋加速器需改变交流电的频率才能加速α粒子.故A错误.
B、根据qvB=m![]() ,知v=
,知v=![]() ,则最大动能EKm=
,则最大动能EKm=![]() mv2=
mv2=![]() .与加速的电压无关.故B错误.
.与加速的电压无关.故B错误.
C、质子出回旋加速器的速度最大,此时的半径为R,则v=![]() =2πRf.所以最大速度不超过2πfR.故C正确.
=2πRf.所以最大速度不超过2πfR.故C正确.
D、粒子在加速电场中做匀加速运动,在磁场中做匀速圆周运动,根据v=![]() 知,质子第二次和第一次经过D形盒狭缝的速度比为
知,质子第二次和第一次经过D形盒狭缝的速度比为![]() :1,
:1,
根据r=![]() ,则半径比为
,则半径比为![]() :1.故D正确.
:1.故D正确.
故选CD.

练习册系列答案
相关题目