题目内容
14.小船匀速横渡一条河流,当船头垂直对岸方向航行时,在出发后l0min到达对岸下游120m处;若船头保持与河岸成θ=53°角向上游航行时,小船恰好能垂直河岸到达正对岸,已知cos53°=0.6,sin53°=0.8,求:(1)水流速度的大小v1.
(2)船在静水中的速度大小v2.
分析 将船的运动分解为垂直于河岸和沿河岸方向,抓住分运动与合运动具有等时性求出河的宽度.
解答 解:(1)设静水速为v1,水流速为v2.船头保持跟河岸垂直的方向航行时有:v2t=120m,
则有:v2=$\frac{120}{10×60}$s=0.2m/s
(2)而v1t=d,当合速度与河岸垂直时,合速度为:
v=$\sqrt{{v}_{1}^{2}-{v}_{2}^{2}}$,
且d=vt′.
联立以上各式解得:d=200m,v1=$\frac{1}{3}$m/s.
答:(1)水流的速度0.2m/s,
(2)船在静水中的速度$\frac{1}{3}$m/s.
点评 解决本题的关键知道分运动与合运动具有等时性,各分运动具有独立性,互不干扰,注意列出方程组,从而求解是解题的基本思路.

练习册系列答案
相关题目
5.关于光电效应,以下说法正确的是( )
| A. | 金属电子的逸出功与入射光的频率无关 | |
| B. | 光电流的强度与入射光的强度有关 | |
| C. | 用红外线照射金属,一定比用可见光照射同种金属产生的光电子的最大初动能大 | |
| D. | 当光照的强度比较弱时,一定要光照射的时间比较长时才能有光电子从金属表面飞出 | |
| E. | 对于任何一种金属都存在一个极限频率,入射光的频率必须大于这个极限频率,才能产生光电效应 |
9.下列说法错误的是( )
| A. | 做曲线运动的物体速度方向必定变化 | |
| B. | 平抛运动是匀变速运动 | |
| C. | 只有曲线运动,才可以对运动进行分解 | |
| D. | 匀速圆周运动属于加速度变化的曲线运动 |
19.如下的说法中,正确的是( )
| A. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$H+${\;}_{0}^{1}$n是轻核聚变反应 | |
| B. | β衰变说明了原子核中有电子 | |
| C. | 光电效应说明了光具有粒子性 | |
| D. | 核反应方程应该遵循质子数和中子数守恒 |
3.关于对牛顿第二定律的理解,下列说法中正确的是( )
| A. | 物体所受的合外力越大,则运动的速度越大 | |
| B. | 物体所受的合外力越大,则运动的速度变化越大 | |
| C. | 物体运动的速度方向与所受合外力方向一致 | |
| D. | 物体运动的加速度方向与所受合外力方向一致 |


 如图,静止于A处的离子,经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强为E0,方向如图所示;离子质量为m、电荷量为q;Q=$\frac{E^2}{R}$t、t=$\frac{L}{{v{\;}_0}}$,离子重力不计
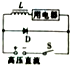
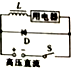
如图,静止于A处的离子,经电压为U的加速电场加速后沿图中圆弧虚线通过静电分析器,从P点垂直CN进入矩形区域的有界匀强电场,电场方向水平向左.静电分析器通道内有均匀辐向分布的电场,已知圆弧所在处场强为E0,方向如图所示;离子质量为m、电荷量为q;Q=$\frac{E^2}{R}$t、t=$\frac{L}{{v{\;}_0}}$,离子重力不计 如图所示,两根足够长的光滑平行金属导轨竖直放置,导轨间距为L,金属导体棒ab垂直放置在导轨上,并与导轨保持良好接触,导体棒电阻为R,导轨电阻不计,空间有垂直导轨平面的匀强磁场,磁感应强度为B.当金属导体棒ab由静止开始向下运动一段时间t0后,再接通开关S,则在下列图象中,导体棒运动的v-t图象可能正确的是( )
如图所示,两根足够长的光滑平行金属导轨竖直放置,导轨间距为L,金属导体棒ab垂直放置在导轨上,并与导轨保持良好接触,导体棒电阻为R,导轨电阻不计,空间有垂直导轨平面的匀强磁场,磁感应强度为B.当金属导体棒ab由静止开始向下运动一段时间t0后,再接通开关S,则在下列图象中,导体棒运动的v-t图象可能正确的是( )


