题目内容
20.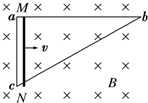 如图所示,直角三角形导线框abc固定在匀强磁场中,ab是一段长为L、电阻为R的均匀导线,ac和bc的电阻可不计,ac长度为$\frac{L}{2}$.磁场的磁感应强度为B,方向垂直纸面向里.现有一段长度为$\frac{L}{2}$,电阻为$\frac{R}{2}$的均匀导体棒MN架在导线框上,开始时紧靠ac,然后沿ab方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触,当MN滑过的距离为$\frac{L}{3}$时,导线ac中的电流多大?
如图所示,直角三角形导线框abc固定在匀强磁场中,ab是一段长为L、电阻为R的均匀导线,ac和bc的电阻可不计,ac长度为$\frac{L}{2}$.磁场的磁感应强度为B,方向垂直纸面向里.现有一段长度为$\frac{L}{2}$,电阻为$\frac{R}{2}$的均匀导体棒MN架在导线框上,开始时紧靠ac,然后沿ab方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触,当MN滑过的距离为$\frac{L}{3}$时,导线ac中的电流多大?
分析 根据公式E=BLv求出图示位置的感应电动势,画出等效电路由欧姆定律求解导线ac中的电流.
解答 解:由几何关系知MP距离为$\frac{L}{3}$,电动势E=$\frac{1}{3}$BLv
MP电阻r=$\frac{1}{3}$R
等效电路如图所示.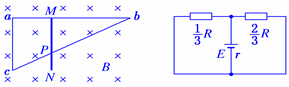
R外=$\frac{2}{9}$R,
电流I=$\frac{E}{{R}_{外}+r}$=$\frac{3BLv}{5R}$,
Iac=$\frac{2}{3}I$=$\frac{2BLv}{5R}$.
答:导线ac中的电流为$\frac{2BLv}{5R}$.
点评 该题把法拉第电磁感应定律与闭合电路的欧姆定律结合在一起考查,是使用电磁感应中的常规题型,该题的关键是接入电流的MP部分的有效长度.

练习册系列答案
相关题目
8.水银气压计中混入了一个气泡,上升到水银柱的上方,使水银柱上方不再是真空.当实际大气压相当于768mm高的水银柱产生的压强时,这个水银气压计的度数只有750mm,此时管中的水银面到管顶的距离为80mm.当这个气压计的读数为740mm水银柱时,实际的大气压强为( )
| A. | 739 mmHg | B. | 756mmHg | C. | 740 mmHg | D. | 758 mmHg |
12.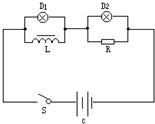 如图所示电路,D1、D2是两个相同的小灯,L是一个自感系数很大的铁芯线圈,其电阻与R相同.由于存在自感现象,在电键S接通和断开时,D1、D2先后亮暗的次序是( )
如图所示电路,D1、D2是两个相同的小灯,L是一个自感系数很大的铁芯线圈,其电阻与R相同.由于存在自感现象,在电键S接通和断开时,D1、D2先后亮暗的次序是( )
 如图所示电路,D1、D2是两个相同的小灯,L是一个自感系数很大的铁芯线圈,其电阻与R相同.由于存在自感现象,在电键S接通和断开时,D1、D2先后亮暗的次序是( )
如图所示电路,D1、D2是两个相同的小灯,L是一个自感系数很大的铁芯线圈,其电阻与R相同.由于存在自感现象,在电键S接通和断开时,D1、D2先后亮暗的次序是( )| A. | 接通时,D1先达最亮 | B. | 接通时,D2先达最亮 | ||
| C. | 断开时,D1后熄灭 | D. | 断开时,D2后熄灭 |
9.下列说法正确的是( )
| A. | 牛顿发现了万有引力定律,并测出了万有引力常量 | |
| B. | 库仑通过扭秤实验确认了真空中两个静止的点电荷之间的相互作用规律 | |
| C. | 楞次发现了电磁感应现象,并研究得出了判断感应电流方向的方法--楞次定律 | |
| D. | 重心、点电荷和交变电流的有效值等概念的建立体现了等效替代的思想 |
10. 氦原子被电离一个核外电子,形成类氢结构的氦离子,已知基态的氦离子能量为E1=-54.4eV,氦离子的能级示意图如图所示.在具有下列能量的光子或者电子中,能被基态氦离子吸收而发生跃迁的是( )
氦原子被电离一个核外电子,形成类氢结构的氦离子,已知基态的氦离子能量为E1=-54.4eV,氦离子的能级示意图如图所示.在具有下列能量的光子或者电子中,能被基态氦离子吸收而发生跃迁的是( )
 氦原子被电离一个核外电子,形成类氢结构的氦离子,已知基态的氦离子能量为E1=-54.4eV,氦离子的能级示意图如图所示.在具有下列能量的光子或者电子中,能被基态氦离子吸收而发生跃迁的是( )
氦原子被电离一个核外电子,形成类氢结构的氦离子,已知基态的氦离子能量为E1=-54.4eV,氦离子的能级示意图如图所示.在具有下列能量的光子或者电子中,能被基态氦离子吸收而发生跃迁的是( )| A. | 42.8 eV(光子) | B. | 43.2 eV(电子) | C. | 41.0 eV(电子) | D. | 54.4 eV(光子) |
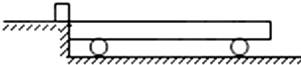
 如图所示为一演示实验电路图,图中L是一带铁芯的线圈,A是一灯泡,电键K处于闭合状态,电路是接通的,现将电键K打开,则在电路切断的瞬间,通过灯泡A的电流方向是从a到b.(填从a到b或从b到a)
如图所示为一演示实验电路图,图中L是一带铁芯的线圈,A是一灯泡,电键K处于闭合状态,电路是接通的,现将电键K打开,则在电路切断的瞬间,通过灯泡A的电流方向是从a到b.(填从a到b或从b到a) 质量为2.0×103kg的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为1.4×104N.
质量为2.0×103kg的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为1.4×104N. 如图为实验室常用的气垫导轨验证动量守恒的装置.在水平放置的气垫导轨上,质量为0.4kg、速度为0.5m/s的滑块A与质量为0.6kg、速度为0.1m/s的滑块B迎面相撞,碰撞前A、B总动量大小是0.14kg•m/s;碰撞后滑块B被弹回的速度大小为0.2m/s,此时滑块A的速度大小为0.05m/s,方向与它原来速度方向相同.(“相同”或“相反”)
如图为实验室常用的气垫导轨验证动量守恒的装置.在水平放置的气垫导轨上,质量为0.4kg、速度为0.5m/s的滑块A与质量为0.6kg、速度为0.1m/s的滑块B迎面相撞,碰撞前A、B总动量大小是0.14kg•m/s;碰撞后滑块B被弹回的速度大小为0.2m/s,此时滑块A的速度大小为0.05m/s,方向与它原来速度方向相同.(“相同”或“相反”)