题目内容
用高电阻放电法测电容的实验,是通过对高阻值电阻放电的方法,测出电容器充电电压为U时,所带的电量为Q,从而再求出待测电容器的电容C.某同学的实验情况如下:
(1)按图甲所示电路连接好实验电路;
(2)接通开关S,调节电阻箱R的阻值,使小量程电流表的指针偏转接近满刻度,记下这时电流表的示数I0=490μA及电压表的示数Uo=6.2V,I0和U0分别是电容器放电的初始电流和电压;
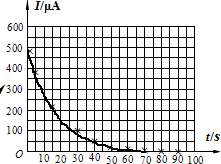
(3)断开开关S,同时开始计时,每隔5s或10s测一次电流I的值,将测得数据填入预先设计的表格中,根据表格中的数据(10组)表示在以时间t为横坐标、电流I为纵坐标的坐标纸上,如图乙中用“×”表示的点.
试根据上述实验结果,在图乙中作出电容器放电的I-t图象,并估算出该电容器两端的电压为U0时所带的电量Q0约为 C;该电容器的电容C约为 F

(1)按图甲所示电路连接好实验电路;
(2)接通开关S,调节电阻箱R的阻值,使小量程电流表的指针偏转接近满刻度,记下这时电流表的示数I0=490μA及电压表的示数Uo=6.2V,I0和U0分别是电容器放电的初始电流和电压;
(3)断开开关S,同时开始计时,每隔5s或10s测一次电流I的值,将测得数据填入预先设计的表格中,根据表格中的数据(10组)表示在以时间t为横坐标、电流I为纵坐标的坐标纸上,如图乙中用“×”表示的点.
试根据上述实验结果,在图乙中作出电容器放电的I-t图象,并估算出该电容器两端的电压为U0时所带的电量Q0约为

分析:由△Q=I?△t知,电荷量为I-t图象与坐标轴所包围的面积,计面积时可数格数(四舍五入).
解答:解:用平滑曲线连接各点,查出所画的曲线与从标轴所围的格数以求得面积.
因△Q=I?△t=t即为曲线与从标轴所围的格数的面积:
则 该电容器两端的电压为U0时所带的电量Q0约为:8.0×10-3C ( 8.0---9.0 )×10-3 C
该电容器的电容C约为:C=
=1.29×10-3F ( 1.29----1.45 )×10-3 F
故答案为:8.0×10-3C ( 8.0---9.0 )×10-3 C 1.29×10-3F ( 1.29----1.45 )×10-3 F
因△Q=I?△t=t即为曲线与从标轴所围的格数的面积:

则 该电容器两端的电压为U0时所带的电量Q0约为:8.0×10-3C ( 8.0---9.0 )×10-3 C
该电容器的电容C约为:C=
| q |
| U0 |
故答案为:8.0×10-3C ( 8.0---9.0 )×10-3 C 1.29×10-3F ( 1.29----1.45 )×10-3 F
点评:考查用数学方法求解物理问题,明确图象的面积的意义.

练习册系列答案
相关题目


|


