题目内容
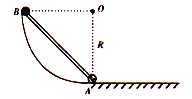
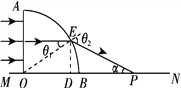
【题目】如图所示，横截面为四分之一圆的柱形玻璃砖放在水平面MN上，O点是圆心，半径为R。一列与OA面等高的平行光束沿水平方向垂直射向玻璃砖的OA面，平行光束通过玻璃砖后在水平面MN上留下照亮的区域。已知玻璃砖的折射率为为n，不考虑光在OA、OB面的反射。
（1）若在玻璃砖左侧竖直放置一遮光板，使水平面BN不被照亮，则遮光板的最小高度是多少？
（2）撤去遮光板，从OA的中点射入的细光束在MN上距O点为
的P点留下一个光点，则玻璃砖的折射率n为多少？
【答案】（1） 
（2）
【解析】试题分析：（1）当光线射到AB面上恰好发生全反射时，遮光板的最小高度等于光线在AB面上的入射以ON的距离，根据折射定律求出临界角，由几何知识求出遮光板的最小高度．（2）作出光路图，根据几何知识确定光线射到AB面上的入射角，由折射定律求出折射率．
(1)当光射到AB面的入射角大于临界角C时，发生全反射，将没有光线射向BN平面。
设遮光板高度为h，由全反射条件得：
由几何知识得：
解得遮光板的最小高度：
(2)如图所示，经OA中点射入的光射到AB面时，入射角为
由
则
故
，解得
折射角
由折射定律
解得：
练习册系列答案
口算能手系列答案
相关题目
