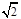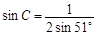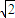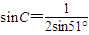题目内容
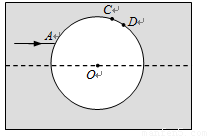
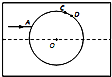
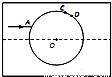
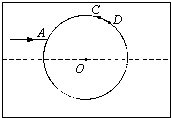 在透明均匀介质内有一球状空气泡,一束包含a、b两种单色光的细光束从介质射入气泡,A为入射点,之后a、b色光分别从C点、D点射向介质,如图所示.已知A点的入射角为30°,a色光的偏向角为45° (C点出射光线与入射光线的夹角),CD弧所对的圆心角为3°,则下列结论正确的是( )
在透明均匀介质内有一球状空气泡,一束包含a、b两种单色光的细光束从介质射入气泡,A为入射点,之后a、b色光分别从C点、D点射向介质,如图所示.已知A点的入射角为30°,a色光的偏向角为45° (C点出射光线与入射光线的夹角),CD弧所对的圆心角为3°,则下列结论正确的是( )分析:设光线在A点的入射角为i,折射角为r,由几何知识知两光束经过球状空气泡偏向角为θ=2(r-i),由a色光的偏向角为45°,可由θ=2(r-i)求出折射角,由折射定律
=
求出折射率.CD弧所对的圆心角为3°,由几何关系求出a色光的折射角,即可求出偏向角,由sinC=
求解临界角.a光的偏向角大于b光的偏向角,a光的折射率大于b光的折射率,a、b两单色光在透明介质中的波长λa<λb.
| 1 |
| n |
| sini |
| sinr |
| 1 |
| n |
解答:解:光线在A点的入射角为i,折射角分别为ra、rb.
A、由a色光的偏向角为45°,而偏向角θa=2(ra-i),得ra=52.5°,由几何知识得:AC弧所对的圆心角为180°-2×52.5°=75°,CD弧所对的圆心角为3°,则AD弧所对的圆心角为78°,故rb=
=51°,b色光的偏向角为θb=2(rb-i)=42°,故A错误.
B、介质对a色光的折射率na=
=
>
=
.故B错误.
C、介质对b色光的折射率nb=
=
,而sinC=
,联立解得,sinC=
.故C正确.
D、由上得知,a光的偏向角大于b光的偏向角,a光的折射率大于b光的折射率,a、b两单色光在透明介质中的波长λa<λb.根据条纹间距公式△x=
λ,波长长的双缝干涉时条纹间距较大,故△xa<△xb故D正确.
故选:CD.
A、由a色光的偏向角为45°,而偏向角θa=2(ra-i),得ra=52.5°,由几何知识得:AC弧所对的圆心角为180°-2×52.5°=75°,CD弧所对的圆心角为3°,则AD弧所对的圆心角为78°,故rb=
| 180°-78° |
| 2 |
B、介质对a色光的折射率na=
| sinra |
| sini |
| sin52.5° |
| sin30° |
| sin45° |
| sin30° |
| 2 |
C、介质对b色光的折射率nb=
| sinrb |
| sini |
| sin51° |
| sin30° |
| 1 |
| n |
| 1 |
| 2sin51° |
D、由上得知,a光的偏向角大于b光的偏向角,a光的折射率大于b光的折射率,a、b两单色光在透明介质中的波长λa<λb.根据条纹间距公式△x=
| L |
| d |
故选:CD.
点评:本题的解题关键是知道偏向角与入射角和折射角的关系,运用几何知识求解光线b的折射角,本题难度较大.

练习册系列答案
相关题目
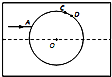 在透明均匀介质内有一球状空气泡,一束包含a、b两种单色光的细光束从介质射入气泡,A为入射点,之后a、b色光分别从C点、D点射向介质,如图所示.已知A点的入射角为30°,a色光的偏向角为45° (C点出射光线与入射光线的夹角),CD弧所对的sin圆心角为3°,则下列结论正确的是( )
在透明均匀介质内有一球状空气泡,一束包含a、b两种单色光的细光束从介质射入气泡,A为入射点,之后a、b色光分别从C点、D点射向介质,如图所示.已知A点的入射角为30°,a色光的偏向角为45° (C点出射光线与入射光线的夹角),CD弧所对的sin圆心角为3°,则下列结论正确的是( )