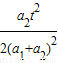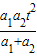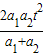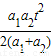Question

一质点由A点静止出发沿直线AB运动，行程的第一部分是加速度大小为a₁的匀加速直线运动，接着做加速度大小为a₂的匀减速直线运动，抵达B点时恰好速度为零．如果质点通过AB段所用的时间为t，AB的总长度为（　　）

• A、

  a2t2

  2(a1+a2)2

• B、

  a1a2t2

  a1+a2

• C、

  a1a2t2

  2(a1+a2)

• D、

  2a1a2t2

  a1+a2

Answer 1

分析：由题物体先做匀加速直线运动，后做匀减速直线运动，根据速度公式得到匀加速运动的时间与总时间t的关系，并求出最大速度，根据平均速度公式求出AB的总长度．

解答：解：设物体匀加速直线运动和匀减速直线运动的时间分别为t₁和t₂，最大速度为v，AB总长度为S．
则有：v=a₁t₁，v=a₂t₂
得到a₁t₁=a₂t₂
由数学知识变形得：

t2

t1

=

a1

a2

，
则

t1+t2

t1

=

a1+a2

a2

而t₁+t₂=t
得到t1=

a2t

a1+a2

，
则t₂=t-t₁=

a1t

a1+a2

，
所以s=

1

2

a1t12+

1

2

a2t22
代入解得s=

a1a2t2

2(a1+a2)

．故C正确，A、B、D错误．
故选：C．

点评：本题涉及两个过程的运动学问题，关键要抓住两个过程之间速度联系．也可以运用作速度图象的方法求解．