题目内容
18. 已知M=200kg的物体,置于升降机内的台秤上,从静止开始上升,运动过程中台秤的示数F与时间t的关系如图所示,(g=10m/s2)求:
已知M=200kg的物体,置于升降机内的台秤上,从静止开始上升,运动过程中台秤的示数F与时间t的关系如图所示,(g=10m/s2)求:(1)升降机在0-2s的加速度?
(2)画出物体整个过程的速度时间图象.
(3)升降机在7s内上升的高度?
分析 (1)根据牛顿第二定律得出0-2s内的加速度.
(2)根据速度时间公式求出2s末的速度,根据支持力和重力的关系得出2-5s内的运动规律,结合5-7s内支持力的大小,根据牛顿第二定律求出加速度,作出速度时间图线.
(3)根据图线围成的面积求出升降机上升的高度.
解答 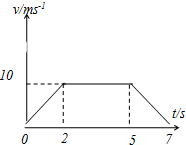 解:(1)设0-2s内的F1=3×103(N),加速度为a1:
解:(1)设0-2s内的F1=3×103(N),加速度为a1:
${a}_{1}=\frac{{F}_{1}-Mg}{M}=\frac{3000-2000}{200}m/{s}^{2}=5m/{s}^{2}$,
(2)0-2s加速后的速度为v:
v=a1t1=5×2m/s=10m/s,
2-5s内支持力等于重力,做匀速直线运动,
设5-7s内的F3=1×103(N),加速度为a3:
${a}_{3}=\frac{{F}_{3}-Mg}{M}=\frac{1000-2000}{200}=-5m/{s}^{2}$,方向向下,
7s末速度为零,速度时间图线如图所示.
(3)7s内上升的高度h即为v-t图所围的面积:
h=$\frac{1}{2}×10×(3+7)m=50m$.
答:(1)升降机在0-2s的加速度为5m/s2;
(2)物体整个过程的速度时间图象如图所示.
(3)升降机在7s内上升的高度为50m.
点评 本题考查了牛顿第二定律和速度时间图线的综合运用,关键理清整个过程中的运动规律,作出速度时间图线,知道图线的斜率表示加速度,图线与时间轴围成的面积表示位移.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.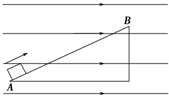 如图所示,水平向右的匀强电场中有一绝缘斜面,一带电金属滑块以Ek0=30J的初动能从斜面底端A冲上斜面,到顶端B时返回,已知滑块从A滑到B的过程中克服摩擦力做功10J,克服重力做功24J,则( )
如图所示,水平向右的匀强电场中有一绝缘斜面,一带电金属滑块以Ek0=30J的初动能从斜面底端A冲上斜面,到顶端B时返回,已知滑块从A滑到B的过程中克服摩擦力做功10J,克服重力做功24J,则( )
 如图所示,水平向右的匀强电场中有一绝缘斜面,一带电金属滑块以Ek0=30J的初动能从斜面底端A冲上斜面,到顶端B时返回,已知滑块从A滑到B的过程中克服摩擦力做功10J,克服重力做功24J,则( )
如图所示,水平向右的匀强电场中有一绝缘斜面,一带电金属滑块以Ek0=30J的初动能从斜面底端A冲上斜面,到顶端B时返回,已知滑块从A滑到B的过程中克服摩擦力做功10J,克服重力做功24J,则( )| A. | 滑块带正电,上滑过程中电势能减小4J | |
| B. | 滑块上滑过程中机械能增加4J | |
| C. | 滑块上滑到斜面中点时重力势能增加12J | |
| D. | 滑块返回到斜面底端时动能为15J |
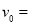 5.0m/s从A点沿倾斜轨道滑下,小物块到达C点时速度
5.0m/s从A点沿倾斜轨道滑下,小物块到达C点时速度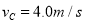 ,取
,取 ,
,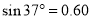 ,
,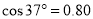
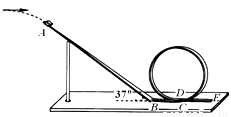
 置于粗糙水平路面上的框架ABCD的质量为M=30kg,其斜面AC的倾角θ=37°,里面放置一表面光滑,质量为m=20kg的球体,框架静止时,球体与顶部AB间有一很小的间隙(间隙远小于球体的半径可忽略不计).整个框架在水平向左的拉力F=400N的作用下向左以v=16m/s的速度做匀速直线运动,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
置于粗糙水平路面上的框架ABCD的质量为M=30kg,其斜面AC的倾角θ=37°,里面放置一表面光滑,质量为m=20kg的球体,框架静止时,球体与顶部AB间有一很小的间隙(间隙远小于球体的半径可忽略不计).整个框架在水平向左的拉力F=400N的作用下向左以v=16m/s的速度做匀速直线运动,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
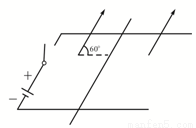
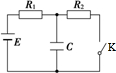 如图所示电路E=10V,R1=4Ω,R2=6Ω,C=30μF,电源内阻可忽略.求:
如图所示电路E=10V,R1=4Ω,R2=6Ω,C=30μF,电源内阻可忽略.求: )求:
)求: