��Ŀ����
����Ŀ����ͼ��ʾ������ֱƽ���ڣ��⻬����AB��ˮƽ��BCƽ��������B�㣬BC�Ҷ������ڱڹ⻬���뾶r=0��2m���ķ�֮һϸԲ��CD��Բ���ھ��Դ���С��ֱ�����ܿ�D�����·�ֱ��һ������ϵ��Ϊk=100N/m���ᵯ�ɣ�����һ�˹̶�����һ��ǡ����ܿ�D��ƽ�룬һ������Ϊ�ʵ��С���������AB�ϣ�С������m=1kg���ִӾ�BC�ĸ߶�Ϊh=0��6m���ɾ�ֹ�ͷ�С������BC��Ķ�Ħ��������=0��5��С�����ܿ�C��ʱ�������Ϲܱ���FN=10N�����������ͨ��CD����ѹ�����ɹ����л����ٶ����ʱ���ɵ�������Ep=0��5J��ȡ�������ٶ�g=10m/s2����
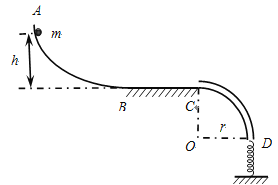
��1��С��ͨ��C��ʱ���ٶȴ�С��
��2��ˮƽ��BC�ij��ȣ�
��3����ѹ�����ɹ�����С��������Ekm
��������1��![]() ����2��
����2��![]() ��3��
��3��![]()
��������
�����������1����С����C�㴦���ٶȴ�СΪ![]() ����ţ�ٵڶ����ɿ�֪��
����ţ�ٵڶ����ɿ�֪��
![]() ��
��![]() ��
��![]() ��
��
��2����BC�ij���ΪS��С���A�˶���C�Ĺ����У��ɶ��ܶ�����֪��
![]()
![]() ��
��
��3����С�������������ڵ��ɵ���ʱ��С���˶��ٶ�������ʱ���ɵ�ѹ����Ϊ![]()
![]()
![]()
С���C���˶����ٶ����Ĺ����У��������غ��֪��
![]() ��
��![]() ��
��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ