题目内容
20．
如图所示，在水平光滑直导轨上，静止着三个质量均为m=1kg的相同小球A、B、C，现让A球以vA=2m/s的速度向着B球运动，A、B两球碰撞后粘合在一起，两球继续向右运动并跟C球碰撞，C球的最终速度vC=1m/s，求：（1）A、B两球碰撞后粘合在一起的速度大小；
（2）A、B两球与C碰撞过程中系统损失的机械能．
分析 （1）碰撞过程系统动量守恒，应用动量守恒定律可以求出碰撞后的速度．
（2）碰撞过程系统动量守恒，应用动量守恒定律可以求出碰撞后的速度，应用能量守恒定律求出损失的机械能．
解答 解：（1）A、B相碰过程系统动量守恒，以向右为正方向，由动量守恒定律得：
mvA=2mv1，
代入数据解得：v1=1m/s；
（2）A、B、C碰撞过程系统动量守恒，以向右为正方向，由动量守恒定律得：
2mv1=mvC+2mv2，
代入数据解得：v2=0.5m/s，
由能量守恒定律可知，B、C碰撞损失的机械能：
△E=$\frac{1}{2}$•2mv12-$\frac{1}{2}$•2mv22-$\frac{1}{2}$mvC2，
代入数据解得：△E=0.25J；
答：（1）A、B两球碰撞后粘合在一起的速度大小为1m/s；
（2）A、B两球与C碰撞过程中系统损失的机械能为0.25J．
点评 本题考查了动量守恒定律与能量守恒定律的应用，分析清楚物体运动过程是正确解题的关键，应用动量守恒定律与能量守恒定律可以解题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．
如图所示，质量相同的两物块A、B用劲度系数为k的轻弹簧连接，静止于光滑水平面上，开始时弹簧处于自然状态，t=0时刻开始，用一水平恒力F拉物块A，使两者做直线运动，经过时间t，弹簧第一次被拉至最长（在弹性限度内），此时物块A的位移为x．则在该过程中，下列说法正确的是（ ）
如图所示，质量相同的两物块A、B用劲度系数为k的轻弹簧连接，静止于光滑水平面上，开始时弹簧处于自然状态，t=0时刻开始，用一水平恒力F拉物块A，使两者做直线运动，经过时间t，弹簧第一次被拉至最长（在弹性限度内），此时物块A的位移为x．则在该过程中，下列说法正确的是（ ）| A． | t时刻，A、B两物块的总动能为Fx | |
| B． | A、B的加速度大小相等时，弹簧的伸长量为$\frac{F}{2k}$ | |
| C． | t时刻突然撤去外力的瞬间，A、B两物块的加速度相同 | |
| D． | A、B的加速度大小相等时，速度大小也一定相等 |
一质量m=0.5kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面，某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度，图示为通过计算机绘制出的滑块上滑过程中的v-t图象，已知sin37°=0.6，cos37°=0.8，g取10m/s2，求：
在某次探究试验中，实验员每次均使某物体以确定的实速率v0沿斜面向上滑出，如图a所示（斜面足够长且与水平方向的倾角θ可在0°-90°之间调节），物体在斜面上能达到的最大位移x与斜面倾角θ的关系由图b中的曲线给出．设各种条件下，物体运动过程中的动摩擦因数μ不变，g=10m/s2，试求：
如图所示，电动机带动滚轮作逆时针匀速转动，在滚轮的摩擦力作用下，将一金属板从斜面底端A送往上部，已知斜面光滑且足够长，倾角θ=30°．滚轮与金属板的切点B到斜面底端A的距离为L=6.5m，当金属板的下端运动到切点B处时，立即提起滚轮使它与板脱离接触．已知金属板返回斜面底部与挡板相撞后立即静止，此时放下滚轮再次压紧板，再次将板从最底端送往斜面上部，如此往复．已知板的质量为m=1×103Kg，滚轮边缘线速度恒为v=4m/s，滚轮对板的正压力FN=2×104N，滚轮与板间的动摩擦因数为μ=0.35，取g=10m/s2．求：
12．如图所示为电场中某区域的电场线分布，下列有关说法中错误的是（ ）
| A． | a点的电势高于b点的电势 | |
| B． | a点的场强大于b点的场强 | |
| C． | 一个正电荷从a点移动到b点，电场力做正功 | |
| D． | 一个负电荷从a点移动到b点，电场力做负功 |
9．关于科学家在电磁学中的贡献，下列说法错误的是（ ）
| A． | 密立根测出了元电荷e的数值 | |
| B． | 法拉第提出了电场线和磁感线的概念 | |
| C． | 奥斯特发现了磁生电 | |
| D． | 安培提出了分子电流假说 |
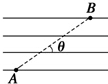一个带正电的微粒，从A点射入水平方向的匀强电场中，微粒沿直线AB运动，如图所示，AB与电场线夹角θ=37°，已知带电微粒的质量m=1.2×10-7kg，电荷量q=1.0×10-10C，A、B相距L=0.3m．（取g=10m/s2）．求：