题目内容
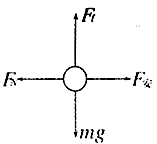
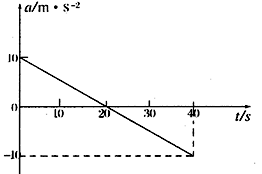
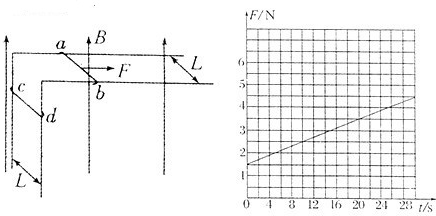
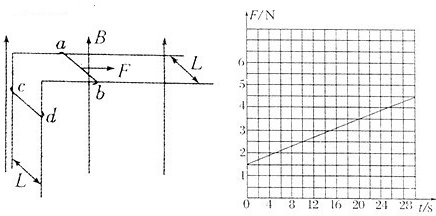
相距为L=0.20m的足够长的金属直角导轨如图所示放置,它们各有一边在同一水平面内,另一边垂直于水平面。质量均为m=1.0kg的金属细杆ab.cd与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数均为μ,导轨电阻不计,回路总电阻为R=1.0Ω。整个装置处于磁感应强度大小为B=0.50T,方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力F作用下从静止开始沿导轨匀加速运动时,cd杆也同时从静止开始沿导轨向下运动。测得拉力F与时间t的关系如图所示。g=10m/s2,求:
(1)杆ab的加速度a和动摩擦因数μ;
(2)杆cd从静止开始沿导轨向下运动达到最大速度所需的时间t0;
|
(1)![]() (2)20s (3)图像见解析
(2)20s (3)图像见解析
解析:
(1)经时间t,杆ab的速率
v=at (1分)
此时,回路中的感应电流为
![]() (1分)
(1分)
对杆ab由牛顿第二定律得
![]() (2分)
(2分)
由以上各式整理得:
![]() (1分)
(1分)
在图线上取两点:![]() ,代入上式得
,代入上式得
![]() (1分)
(1分)
![]() (1分)
(1分)
|
![]() (2分)
(2分)
又FN=F安 (1分)
F安=BIL (1分)
![]() (1分)
(1分)
![]() (1分)
(1分)
整理解得![]() (1分)
(1分)
|

练习册系列答案
相关题目