题目内容
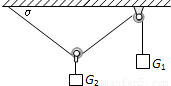
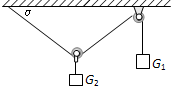 已知如图,一根轻绳左端固定在水平天花板上,依次穿过不计质量和摩擦的动滑轮和定滑轮后,悬挂重G1的物体A,在动滑轮下悬挂重G2的物体B,系统处于静止状态.求:
已知如图,一根轻绳左端固定在水平天花板上,依次穿过不计质量和摩擦的动滑轮和定滑轮后,悬挂重G1的物体A,在动滑轮下悬挂重G2的物体B,系统处于静止状态.求:(1)若G1=G2=10N,静止时细绳与天花板间的夹角α=?
(2)若测得G1=10N,α=37°,那么G2=?
分析:对m1进行受力分析,求出绳子的拉力大小;对滑轮进行分析,由于滑轮放在一根绳子上,绳子两端的张力相等,然后由共点力的平衡关系根据两物体间的质量关系求出夹角.
解答:解:(1)以m1为研究对象,A受竖直向下的重力G1、竖直向上的绳子拉力F,处于平衡状态,由平衡条件得:F=G1;
以动滑轮为研究对象,动滑轮受物体B竖直向下拉力G2、绳子的两个拉力F作用,绳子的两个拉力相等,绳子拉力的合力一定两绳子夹角的角平分线上,动滑轮静止,处于平衡状态,绳子拉力的合力等于G2,两绳子的拉力等于G1,
根据力的合成与平衡条件有:2G1sinα=G2
解得:α=30°
(2)2G1sinα=G2
代入数据得:G2=12N.
答:(1)若G1=G2=10N,静止时细绳与天花板间的夹角α=30°.
(2)若测得G1=10N,α=37°,那么G2=12N.
以动滑轮为研究对象,动滑轮受物体B竖直向下拉力G2、绳子的两个拉力F作用,绳子的两个拉力相等,绳子拉力的合力一定两绳子夹角的角平分线上,动滑轮静止,处于平衡状态,绳子拉力的合力等于G2,两绳子的拉力等于G1,
根据力的合成与平衡条件有:2G1sinα=G2
解得:α=30°
(2)2G1sinα=G2
代入数据得:G2=12N.
答:(1)若G1=G2=10N,静止时细绳与天花板间的夹角α=30°.
(2)若测得G1=10N,α=37°,那么G2=12N.
点评:本题中要注意题目隐含的信息,记住同一绳子各部分的张力相等,即可由几何关系得出夹角的关系

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
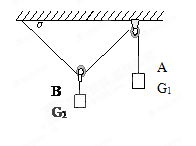
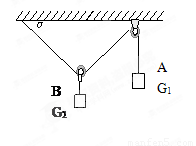
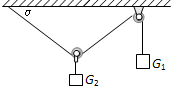 已知如图,一根轻绳左端固定在水平天花板上,依次穿过不计质量和摩擦的动滑轮和定滑轮后,悬挂重G1的物体A,在动滑轮下悬挂重G2的物体B,系统处于静止状态.求:
已知如图,一根轻绳左端固定在水平天花板上,依次穿过不计质量和摩擦的动滑轮和定滑轮后,悬挂重G1的物体A,在动滑轮下悬挂重G2的物体B,系统处于静止状态.求: