题目内容
【题目】如图所示，在坐标系xOy平面的x>0区域内，存在电场强度大小E=2×105N／C、方向垂直于x轴的匀强电场和磁感应强度大小B=0.20 T、方向与xOy平面垂直向外的匀强磁场。在y轴上有一足够长的荧光屏PQ，在x轴上的M(10，0)点处有一粒子发射枪向x轴正方向连续不断地发射大量质量m=6.4×10-27kg、电荷量q=3.2×10-19C的带正电粒子(重力不计)，粒子恰能沿x轴做匀速直线运动。若撤去电场，并使粒子发射枪以M点为轴在xOy平面内以角速度
顺时针匀速转动(整个装置都处在真空中)。
(1)判断电场方向，求粒子离开发射枪时的速度；
(2)带电粒子在磁场中运动的轨迹半径；
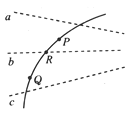
(3)荧光屏上闪光点的范围；
(4)若不考虑粒子在磁场中的运动时间，求荧光屏上闪光点从最低点移动到最高点所用的时间。
【答案】（1）106m/s；（2）0.1m；（3）0.273m；（4）0.42s；
【解析】试题分析：（1）粒子做匀速直线运动，所受合力为零，由平衡条件可以求出粒子的运动速度；粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律列方程可以求出粒子的轨道半径，（2）根据题意作出粒子打在荧光屏上的范围图示，然后由数学知识求出荧光屏上闪光点的范围，（3）求出粒子在磁场中做圆周运动的周期，求出粒子运动的圆心角，最后求出粒子的运动时间。
(1)根据粒子恰能沿x轴做匀速直线运动，粒子受到竖直向下的洛伦兹力，则电场力应竖直向上，所以电场强度方向竖直向上，根据
可得
，代入数据得
；
(2) 撤去电场后，有： 
，粒子在磁场中运动的轨迹半径
，代入数据得：R=0.1m；
(3) 粒子运动轨迹可知，粒子最上端打在A点，最下端打在B点： 
， 
， 
；
(4 )粒子在磁场中做圆周运动的周期： 
，粒子在磁场中运动的时间可以忽略不计，闪光点从最高点移到最低点的过程中，粒子枪转过的圆心角为
，所以时间为
。
点晴：粒子做匀速圆周运动，由平衡条件可以求出粒子的运动速度，粒子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律列方程，可以求出粒子运动的轨道半径；求出粒子在磁场中做圆周运动所转过的圆心角是求出粒子在磁场中运动时间的关键；第三问是本题的难点，根据题意作出粒子的运动轨迹是解题的关键。
