Question

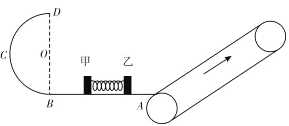
【题目】如图所示，倾角为37°足够长的传送带顺时针转动速度为v0=2m/s，左边是光滑竖直半圆轨道，半径R=0.8m，中间是光滑的水平面AB（足够长），AB与传送带在A点由一段圆弧连接。用轻质细线连接甲、乙两物体，两物体中间夹一轻质弹簧，弹簧与甲、乙两物体不拴连。甲的质量为m1=3kg，乙的质量为m2=1kg，甲、乙均静止在光滑的水平面上。现固定甲物体，烧断细线，乙物体离开弹簧后在传送带上滑行的最远距离为s=8m。传送带与乙物体间的动摩擦因数为0.5，重力加速度g取10m/s2，甲、乙两物体可看作质点。（sin37°=0.6，cos37°= 0.8）

(1)求物体乙刚滑上传送带时的速度；

(2)若固定乙物体，烧断细线，甲物体离开弹簧后进入半圆轨道，求甲物体通过D点时对轨道的压力大小；

(3)甲、乙两物体均不固定，烧断细线以后，试通过计算判断甲物体进人半圆轨道后是否会脱离圆弧轨道。

Answer 1

【答案】(1)12m/s；(2)30N；(3)不会脱离

【解析】

(1)乙物体滑上传送带做匀减速运动，开始时

共速之后的加速度

由运动公式

解得

v=12m/s

(2)由机械能守恒定律可得弹簧压缩时的弹性势能

固定乙物体，烧断细线，甲物体离开弹簧时的速度满足

物体甲到达D点的过程机械能守恒

甲物体在D点有

解得

FND=30N

(3)甲乙两物体均不固定，烧断细线后，根据能量守恒定律

由动量守恒

解得

，

之后甲物体沿轨道上滑，设上滑的最大高度为h，则

解得

甲物体滑不到与圆心等高的位置就会返回，所以不会脱离圆弧轨道。