��Ŀ����
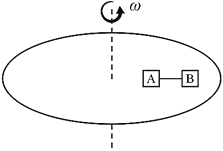
����Ŀ����ͼ��ʾ������Ϊ1kg��С���ڹ̶���ֱ���ϣ�����ˮƽ�����37��ǣ�����˼�Ķ�Ħ��������=0.5��С������ֱ���ϵĴ�СΪ20N������F�����£�����˵��¶�0.24m���ɾ�ֹ��ʼ�����˶�������1s��ȥ������ȡg=10m/s2 �� sin37��=0.6��cos37��=0.8����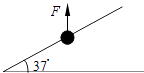
��1��С���ظ��ϻ��ļ��ٶȴ�С��
��2��С���ظ��ϻ��������룻
��3��С��Ӿ�ֹ���˵��¶������ʱ�䣮
���𰸡�
��1���⣺���������ţ�ٵڶ������У���F��mg��sin37�㩁�̣�F��mg��cos37��=ma1
���С���ϻ��ļ��ٶȴ�СΪ��a1=2m/s2
��С���ظ��ϻ��ļ��ٶȴ�СΪ2m/s2��
��2���⣺�����˶�ѧ�����У�
v1=a1t1=2��1m/s=2m/s
![]()
��ȥ������С����������˶�������ţ�ٵڶ����ɣ�
mgsin37��+��mgcos37��=ma2
��ã�a2=10m/s2
![]()
�������ϸ�ʽ���С���ظ��ϻ���������Ϊ��x=x1+x2=1m+0.2m=1.2m
��С���ظ��ϻ���������Ϊ1.2m��
��3���⣺С���˶�����ߵ��ʼ�»����У� ![]()
����ţ�ٵڶ������У�mgsin37�㩁��mgcos37��=ma3
����λ��ʱ���ϵ�У� ![]()
������ã�a3=2m/s��t3=1.2s
С��Ӿ�ֹ���˵��¶������ʱ��Ϊ��t=t1+t2+t3=2.4s
��С��Ӿ�ֹ���˵��¶������ʱ��Ϊ2.4s��
����������1����������������������ţ�ٵڶ����ɿ���ü��ٶȣ���2�������ٶȹ�ʽ����ó�ȥ����ʱ���ٶȺ�λ�ƣ��ٶԳ�ȥ�������̽��з���������ţ�ٵڶ����ɿ���ü��ٶȣ��ٸ����ٶȺ�λ�ƵĹ�ϵ���λ�ƣ����������λ�ƣ���3���»����̸���ţ�ٵڶ����ɿ���ü��ٶȣ��ٽ���˶�ѧ��ʽ���ʱ�䣮

 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�