题目内容
13．
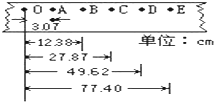某次实验纸带的记录如图所示，图中前几个点模糊，因此从O点开始每打5个点取1个计数点，则小车通过D点时速度是2.46m/s，小车运动的加速度是6.2m/s2．（打点计时器的电源频率是50Hz）
分析 根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上D点时小车的瞬时速度大小．
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小．
解答 解：从A点开始每打5个点取1个计数点，相邻的计数点之间的时间间隔是0.1s
（1）根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，
vD=$\frac{{x}_{CE}}{{t}_{CE}}$=$\frac{0.7740-0.2787}{2×0.1}$m/s=2.46m/s
（2）逐差法求解：
a=$\frac{{x}_{CE}-{x}_{AC}}{4{T}^{2}}$=6.2m/s2；
故答案为：2.46；6.2．
点评 本题考查了打点计时器的应用以及根据纸带求物体运动的速度、加速度等问题，要熟练掌握从纸带上获取小车速度、加速度的方法．要注意单位的换算．
练习册系列答案
相关题目
如图所示，在光滑水平面上有质量均为m的A、B两物体，在水平面的右端有一轻弹簧，弹簧的右端固定在水平面右端的墙壁上，且A、B与弹簧在同一条水平线上，现给A向右的初速度v0使其向B运动并与B碰撞，碰后A、B粘在一起向弹簧运动，设在整个A、B与弹簧作用的过程中，弹簧都在弹性限度内，求弹簧在相互作用过程中的最大弹性势能Epm．
4．
一台小型发电机产生的电动势随时间变化的规律为e=220$\sqrt{2}$sin100πtV．已知发电机线圈内阻为5.0Ω，外接一个电阻为95.0Ω 的灯泡，如图所示，则（ ）
一台小型发电机产生的电动势随时间变化的规律为e=220$\sqrt{2}$sin100πtV．已知发电机线圈内阻为5.0Ω，外接一个电阻为95.0Ω 的灯泡，如图所示，则（ ）| A． | 交流电压表的示数为220$\sqrt{2}$V | |
| B． | 该交流电压的频率为100Hz | |
| C． | 线框在如图位置时，穿过线框的磁通量最大 | |
| D． | 发电机线圈内阻每秒钟产生的焦耳热为24.2J |
1．质点沿两个半径均为R的半圆弧由A运动到C，如图所示，则其路程和位移分别是（ ）
| A． | 0；0 | B． | 4R、方向向东；2πR、方向向东 | ||
| C． | 2πR；4R、方向向东 | D． | 2πR；4R |
5．关于运动状态与所受外力的关系，正确的是（ ）
| A． | 物体受到的合外力为零时，物体一定做匀速直线运动 | |
| B． | 物体受到的合外力不为零时，物体一定做变速运动 | |
| C． | 物体受到不为零的恒定合外力时，物体一定做匀变速运动 | |
| D． | 物体受到的合外力方向，就是物体的运动方向 |
2．
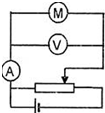实际生活中，我们常常要选用参数恰当的元件，某同学用如图所示的电路进行小电机M的输出功率的研究（图中电表均为理想仪表），其实验步骤如下所述：连接好电路后，调节滑动变阻器，电动机未转动时，电压表的读数为U1，电流表的读数为I1；再调节滑动变阻器，电动机转动后电压表的读数为U2，电流表的读数为I2，则此时电动机的输出功率（ ）
实际生活中，我们常常要选用参数恰当的元件，某同学用如图所示的电路进行小电机M的输出功率的研究（图中电表均为理想仪表），其实验步骤如下所述：连接好电路后，调节滑动变阻器，电动机未转动时，电压表的读数为U1，电流表的读数为I1；再调节滑动变阻器，电动机转动后电压表的读数为U2，电流表的读数为I2，则此时电动机的输出功率（ ）| A． | U2I2-U1I1 | B． | U2I2-I22$\frac{U_1}{I_1}$ | C． | U2I2+I22$\frac{U_1}{I_1}$ | D． | I22$\frac{U_1}{I_1}$ |
3．一质点做匀加速直线运动，通过A点时速度为vA，经过时间t通过B点，速度为vB，又经过相同时间t通过C点，速度为vC，则以下关系式错误的是（ ）
| A． | vB=$\frac{1}{2}$（vA+vC） | B． | vB=$\frac{1}{2t}$（AB+BC） | C． | a=$\frac{1}{2t}$（vC-vA） | D． | a=$\frac{1}{2{t}^{2}}$（BC-AB） |