题目内容
如图所示,小车的质量为M=3kg,车的上表面左端为
光滑圆弧BC,右端为水平粗糙平面AB,二者相切于B点,AB的长为L=4m,一质量为m=1kg的小物块,放在车的最右端,小物块与车之间的动摩擦因数为μ=0.10.车和小物块一起以v0=4m/s的速度在光滑水平面上匀速向左运动,小车撞墙后瞬间速度变为零,但未与墙粘连.g取10m/s2,求:
(1)小物块沿圆弧上升的最大高度为多少?
(2)小物块从最高点返回后与车的速度相同时,小物块距B端多远.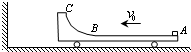
| 1 |
| 4 |
(1)小物块沿圆弧上升的最大高度为多少?
(2)小物块从最高点返回后与车的速度相同时,小物块距B端多远.

(1)小物块从开始到上升到最高点的过程中,
由能量守恒定律得:mgh=
m
-μmgL,
解得:h=0.4m;
(2)物块从开始返回B点过程,
由动能定理得:-μmgL=
mv12-
mv02,
解得:v1=2
m/s,
物块从B向右滑行过程中,
由动量守恒定律得:mv1=(M+m)v2,
解得v2=
m/s,
由能量守恒定律得:
mv12-
(M+m)v22=μmgL1,
解得:L1=3m.
答:(1)小物块沿圆弧上升的最大高度为0.4m.
(2)小物块从最高点返回后与车的速度相同时,小物块距B端3m.
由能量守恒定律得:mgh=
| 1 |
| 2 |
| v | 20 |
解得:h=0.4m;
(2)物块从开始返回B点过程,
由动能定理得:-μmgL=
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1=2
| 2 |
物块从B向右滑行过程中,
由动量守恒定律得:mv1=(M+m)v2,
解得v2=
| ||
| 2 |
由能量守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:L1=3m.
答:(1)小物块沿圆弧上升的最大高度为0.4m.
(2)小物块从最高点返回后与车的速度相同时,小物块距B端3m.

练习册系列答案
相关题目
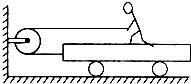 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力不可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力不可能是( )| A、0 | ||
B、(
| ||
C、(
| ||
D、(
|
 如图所示,小车的质量为M,正在向右加速运动,一个质量为m的木块紧靠在车的前端相对于车保持静止,则下列说法正确的是( )
如图所示,小车的质量为M,正在向右加速运动,一个质量为m的木块紧靠在车的前端相对于车保持静止,则下列说法正确的是( ) 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,不计滑轮与绳的质量,则车对人的摩擦力大小和方向不可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,不计滑轮与绳的质量,则车对人的摩擦力大小和方向不可能是( ) 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力可能是( ) 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面光滑,不计滑轮与绳的质量,则车对人的摩擦力可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面光滑,不计滑轮与绳的质量,则车对人的摩擦力可能是( )