Question

【题目】天文工作者测得某行星的半径为R1．它有一颗绕其做圆周运动卫星，卫星轨道半径为R2，卫星运行周期为T．已知万有引力常量为G．

（1）求该颗卫星加速度；

（2）求该行星的平均密度；

（3）要在该星球上发射一颗靠近表面运行的人造卫星，此卫星的速度为多大？

Answer 1

【答案】（1）；

（2）；

（3）

【解析】试题分析：（1）卫星绕行星做的是匀速圆周运动，结合轨道半径和周期求出卫星加速度；

（2）根据万有引力提供向心力，由牛顿第二定律求出行星的质量．再求行星的平均密度．

（3）根据行星表面万有引力提供向心力求解第一宇宙速度，即为此卫星的速度．

解：（1）卫星绕行星做圆周运动，其加速度为：a=

（2）根据万有引力提供向心力，由牛顿第二定律得：

G=m

可得行星的质量为：M=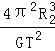

因此该行星的平均密度为：ρ===

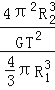（3）靠近行星表面运行的人造卫星的轨道半径近似等于行星的半径R1．由万有引力提供向心力，得

G=m

联立解得：v=

答：（1）该颗卫星加速度是；

（2）该行星的平均密度是；

（3）要在该星球上发射一颗靠近表面运行的人造卫星，此卫星的速度为．