Question

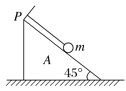
【题目】如图所示，细线的一端固定在倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球．则（ ）

A. 当滑块静止时，绳的拉力大小为

B. 当滑块向右以a=g做匀加速直线运动时，细线的拉力大小为零

C. 当滑块向左以a=g做匀加速直线运动时，细线的拉力大小为

D. 当滑块向右以做匀加速直线运动时，细线的拉力大小为2mg

Answer 1

【答案】BC

【解析】A、当滑块和小球静止时，根据共点力平衡求得 故A错误.B、C、当小球贴着滑块一起向左运动时，小球受到重力、拉力和支持力作用，在这三个力作用下产生向左的加速度．当滑块向左运动的加速度增大到一定值时，小球可能抛起，斜面对滑块的支持力为零，小球受重力和拉力两个力作用．如图所示：

将小球所受的力沿加速度方向和垂直于加速度方向分解，有：Tcos45°-Nsin45°=ma，Tsin45°+Ncos45°=mg，而a=g时，N=0，此时，线中拉力,故C均正确。B、D、当斜面体以向右匀加速直线运动时，对小球受力分析如图：

小球可能会相对斜面向后滑动，根据牛顿第二定律，知小球的加速度，则绳的拉力为零，而向右时，小球已经相对斜面向左滑动，绳未拉直，绳的拉力一直为零，故B正确、D错误.故选BC.