题目内容
在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内作水平面上的匀速圆周运动,并与圆锥内壁接触。如图所示,图(a)中小环与小球在同一水平面上,图(b)中轻绳与竖直轴成θ角。设a图和b图中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )

①Ta一定为零,Tb一定为 零
②Ta可以为零,Tb可以不为零
③Na一定不为零,Nb可以为零
④Na可以为零,Nb 可以不为零
A.①③ B.②③ C.①④ D.②④
【答案】
B
【解析】
试题分析:物体做圆周运动,关键是有没有合适的向心力,因此在a图中,小球恰好与圆锥接触,但是没有产生弹力,所以是有可能做匀速圆周运动,所以2是正确的。所以排除AC。在b图中,绳子拉力也可以为零,靠支持力和重力提供指向圆心的合外力,因此排除4,综上所述,答案为B
考点:向心力
点评:本题考查了受力分析,即向心力来源问题的受力分析。根据圆周运动的特点,需要指向圆心的合外力或者分力。

练习册系列答案
相关题目
 在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内作水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图(a)中小环与小球在同一水平面上,图(b)中轻绳与竖直轴成θ(θ<90°)角.设a图和b图中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )
在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内作水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图(a)中小环与小球在同一水平面上,图(b)中轻绳与竖直轴成θ(θ<90°)角.设a图和b图中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )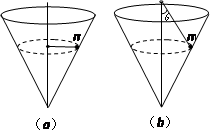
 的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图①中小环与小球在同一水平面上,图②中轻绳与竖直轴成
的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图①中小环与小球在同一水平面上,图②中轻绳与竖直轴成 角.设图①和图②中轻绳对小球的拉力分别为
角.设图①和图②中轻绳对小球的拉力分别为 和
和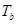 ,圆锥内壁对小球的支持力分别为
,圆锥内壁对小球的支持力分别为 和
和 ,则下列说法中正确的是( )
,则下列说法中正确的是( ) 
