题目内容
【题目】如图所示，在直角坐标系xOy中，板间距离为d的正对金属板M、N上有两个小孔S、K，S、K均在y轴（竖直）上。在以原点O为圆心、以R为半径的圆形区域内存在方向垂直纸面向外的匀强磁场，圆O与M板相切于S、与x负半轴相交于C点。小孔K处的灯丝不断地逸出质量为m、电荷量为e的电子（初速度和重力均不计），电子在两板间的电场作用下沿y轴正方向运动。当M、N间的电压为
时，从小孔K逸出的电子恰好通过C点。
（1）求电子到达小孔S处时的速度大小
；
（2）求磁场的磁感应强度大小B；
（3）若M、N间的电压增大为
，求从小孔K逸出的电子离开磁场时的位置D（图中未画）的坐标。
【答案】（1）
（2）
（3）
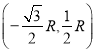
【解析】
（1）电子的运动轨迹如图所示，在电子从小孔K运动到小孔S的过程中，根据动能定理有：
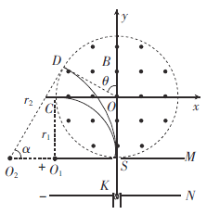
解得：
（2）当电子恰好通过C点时，根据几何关系可得电子在磁场中的轨道半径为：
洛伦兹力提供电子做圆周运动所需的向心力，有：
解得：
（3）设此种情况下电子到达小孔S处时的速度大小为v，根据动能定理有：
设此种情况下电子在磁场中的轨道半径为
，有：
解得：
设O、D两点连线与y轴的夹角为θ，由几何关系知，此种情况下电子从小孔S运动到D点的轨迹（圆弧）对应的圆心角为：
由几何关系有：
解得：
故D点的位置坐标为
，即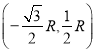
练习册系列答案
相关题目
