题目内容
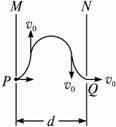
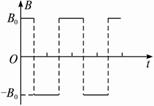
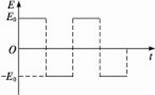
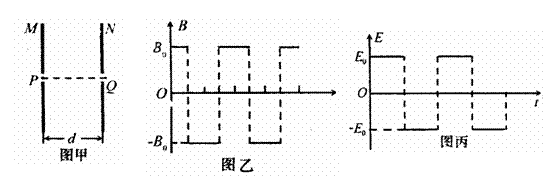
如图所示，一对平行放置的金属板M、N的中心各有一小孔P、Q，PQ连线垂直金属板；N板右侧的圆形区域A内分布有方向垂直于纸面向外的匀强磁场，磁感应强度大小为B，圆半径为r，且圆心O在PQ的延长线上，两平行金属板与匝数为n，边长为a的正方形线圈相连，现有垂直于线圈平面均匀增大的磁场，磁感应强度变化率为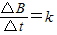
，一质量为m、电量为q的带负电粒子（重力不计），初速度为零，从P点进入两板间，求：（1）两平行板之间的电势差
（2）粒子从Q点射出时的速度
（3）带电粒子通过该圆形磁场的偏转角θ
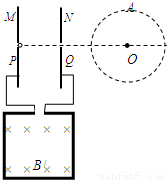
【答案】分析：（1）线圈与磁场垂直，磁场的B均匀增大时，线圈中产生恒定的感应电动势，由法拉第定律求出感应电动势，因线圈中没有电流，两平行板间的电压等于感应电动势．
（2）粒子在电场中加速，运用动能定理求粒子从Q点射出时的速度．
（3）粒子进入偏转磁场，做匀速圆周运动，画出轨迹，由牛顿第二定律求出轨迹半径，即可由几何知识求偏转角θ．
解答：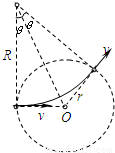
解（1）根据法拉第电磁感应定律 E=n
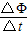=n
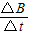a2=nka2
所以，两板间电压为：U=E=nka2
（2）粒子在电场中加速，由动能定理得：qU=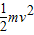
所以，粒子射出两极板时的速度：v=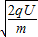
=
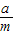
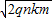
（3）粒子进入偏转磁场，如图所示，设偏转角为θ，粒子做圆周运动的半径为R，由几何关系有：tan
=
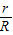
由牛顿第二定律：qvB=m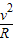
化简得：tan
=
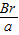
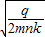
即：θ=2arctan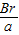
．
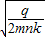答：
（1）两平行板之间的电势差为nka2．
（2）粒子从Q点射出时的速度为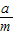
．
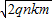（3）带电粒子通过该圆形磁场的偏转角θ为2arctan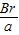
．
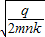点评：本题是电磁感应、电场加速和磁场偏转的组合，要掌握每个过程相关的解题规律，关键要画出磁场中粒子的运动轨迹，运用几何知识求解偏转角θ．
（2）粒子在电场中加速，运用动能定理求粒子从Q点射出时的速度．
（3）粒子进入偏转磁场，做匀速圆周运动，画出轨迹，由牛顿第二定律求出轨迹半径，即可由几何知识求偏转角θ．
解答：
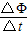解（1）根据法拉第电磁感应定律 E=n=n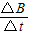a2=nka2所以，两板间电压为：U=E=nka2
（2）粒子在电场中加速，由动能定理得：qU=
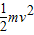
所以，粒子射出两极板时的速度：v=
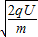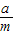
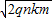
=（3）粒子进入偏转磁场，如图所示，设偏转角为θ，粒子做圆周运动的半径为R，由几何关系有：tan
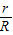
= 由牛顿第二定律：qvB=m
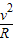
化简得：tan
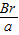
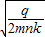
=即：θ=2arctan
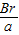
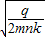．答：
（1）两平行板之间的电势差为nka2．
（2）粒子从Q点射出时的速度为
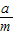
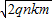．（3）带电粒子通过该圆形磁场的偏转角θ为2arctan
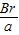
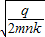．点评：本题是电磁感应、电场加速和磁场偏转的组合，要掌握每个过程相关的解题规律，关键要画出磁场中粒子的运动轨迹，运用几何知识求解偏转角θ．
练习册系列答案
相关题目
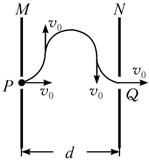
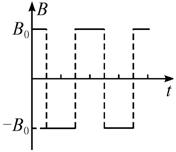
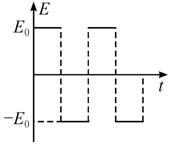
如图所示，水平桌面上放着一对平行金属导轨，左端与一电源相连，中间还串有一开关K．导轨上放着一根金属棒ab，空间存在着匀强磁场．已知两导轨间距为d，电源电动势为E，导轨电阻及电源内阻均不计，ab棒的电阻为R，质量为m，棒与导轨间摩擦不计．闭合开关K，ab棒向右运动并从桌边水平飞出，已知桌面离地高度为h，金属棒落地点的水平位移为s．下面的结论中正确是
射入磁场，正好垂直于N板从Q孔射出磁场。已知粒子在磁场中做匀速圆周运动的时间恰为一个周 期，且与磁感应强度变化的周期相同，求
个周期的时间内放出的带电粒子才能从小孔Q处射出，求这些带电粒子到达Q孔处的速度范围。
射入磁场，正好垂直于N板从Q孔射出磁场。已知粒子在磁场中做匀速圆周运动的时间恰为一个周 期，且与磁感应强度变化的周期相同，求
个周期的时间内放出的带电粒子才能从小孔Q处射出，求这些带电粒子到达Q孔处的速度范围。