ЬтФПФкШн
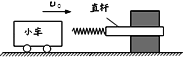
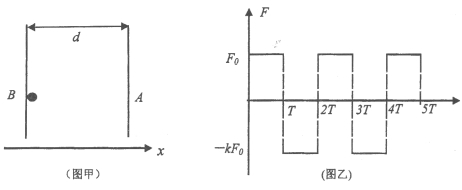
ЁОЬтФПЁПвЛЮяПщAгЩОВжЙЪЭЗХвдМгЫйЖШa=2m/s2биаБУцBЃЈаБУцЮоЯоГЄЃЉЯђЯТдЫЖЏ5sКѓЃЌМгбиаБУцЯђЩЯЕФСІF1=50NзїгУЪБМф4sЃЌвбжЊAЕФжЪСПm=10kgЃЌBЕФжЪСПM=20kgЃЌgШЁ10m/s2ЃЌаБУцНЧЖШІС=37ЁуЃЈsin37Ёу=0.6ЃЌcos37Ёу=0.8ЃЉЙ§ГЬжааБУцОВжЙЃЎ

ЃЈ1ЃЉЧѓаБУцЕФФІВСвђЪ§ІЬЃЛ
ЃЈ2ЃЉЧѓF1зїгУЪБМфФкЕФЮЛвЦЃЛ
ЃЈ3ЃЉЧѓЧА5УыФкЕиУцИјаБУцЕФжЇГжСІFNгыФІВССІfЕФДѓаЁКЭЗНЯђЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0.5 ЃЈ2ЃЉ16.7m ЃЈ3ЃЉ288NЪњжБЯђЩЯ 16N ЫЎЦНЯђзѓ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЖдЮяЬхЪмСІЗжЮідкгЩХЃЖйЕкЖўЖЈТЩПЩвдЧѓГіЖЏФІВСвђЪ§ЃЌЮяПщЯШзідШМгЫйжБЯпдЫЖЏЃЌМгЩЯСІF1КѓзідШМѕЫйжБЯпдЫЖЏЃЌгІгУХЃЖйЕкЖўЖЈТЩгыдЫЖЏбЇЙЋЪНЧѓГіЮяПщЕФЮЛвЦЃЛвђЮЊаБУцBОВжЙЃЌгЩЦНКтЬѕМўПЩвдЧѓГіжЇГжСІгыФІВССІЁЃ
ЃЈ1ЃЉЖдЮяПщAЪмСІЗжЮіЃЌгЩХЃЖйЕкЖўЖЈТЩЕУЃК ![]() ЃЌ
ЃЌ
ДјШыЪ§ОнНтЕУЃКІЬ=0.5ЃЛ
ЃЈ2ЃЉИљОнЫйЖШгыЪБМфЙиЯЕПЩЕУ5sФЉЮяПщAЕФЫйЖШЃКv1=at0=2ЁС5=10m/s
ЕБF1зїгУдкAЩЯЪБЃЌгЩХЃЖйЕкЖўЖЈТЩЕУЃК ![]()
ДјШыЪ§ОнНтЕУЃКa1=3m/s2
ЮяПщМѕЫйЕНЫйЖШЮЊСуашвЊЕФЪБМфЃК ![]()
ЫљОЙ§ЕФЮЛвЦЮЊЃК ![]()
ЃЈ3ЃЉЮяЬхAЪмЕНЕФЛЌЖЏФІВССІЃКfA=ІЬmgcosІШ=0.5ЁС10ЁС10cos37Ёу=40NЃЌ
вђЮЊаБУцMОВжЙЃЌгЩЦНКтЬѕМўЕУЃЌЪњжБЗНЯђЃК ![]()
ДјШыЪ§ОнНтЕУЃК ![]() ЗНЯђЪњжБЯђЩЯ
ЗНЯђЪњжБЯђЩЯ
дкЫЎЦНЗНЯђгаЃК ![]()
ДјШыЪ§ОнНтЕУЃКf=16NЃЌЗНЯђЃКЫЎЦНЯђзѓЁЃ