题目内容
(1)如图1所示为两列简谐横波在同一绳上传播在t=0时刻的波形图,已知甲波向左传,乙波向右传.请根据图中信息判断以下说法正确的是
A.两列波的波长一样大
B.甲波的频率f1比乙波的频率f2大
C.由于两波振幅不等,故两列波相遇时不会发生干涉现象
D.两列波同时传到坐标原点
E.x=0.2cm处的质点开始振动时的方向向-y方向
F.两列波相遇时会发生干涉且x=0.5cm处为振动加强的点
(2)如图2所示,折射率n=
的半圆形玻璃砖置于光屏MN的上方,其平面AB到MN的距离为h=10cm.一束单色光沿图示方向射向圆心O,经玻璃砖后射到光屏上的O′点.现使玻璃砖绕圆心O点顺时针转动,光屏上的光点将向哪个方向移动?光点离O′点最远是多少?

ADF
ADF
A.两列波的波长一样大
B.甲波的频率f1比乙波的频率f2大
C.由于两波振幅不等,故两列波相遇时不会发生干涉现象
D.两列波同时传到坐标原点
E.x=0.2cm处的质点开始振动时的方向向-y方向
F.两列波相遇时会发生干涉且x=0.5cm处为振动加强的点
(2)如图2所示,折射率n=
| 2 |

分析:(1)根据相邻波峰或波谷间的距离等于波长,直接比较波长的大小;两列波的波速相同,由波速公式v=λf分析频率关系;若两列波的频率相同,就能够发生干涉;介质中各点的起振方向与波最前头的起振方向相同,由波的传播方向判断;
(2)使玻璃砖绕圆心O点顺时针转动,相当于玻璃砖不动,入射光线逆时针,出射光线也逆时针转动,可知光点向右移动.由全反射知识及几何知识可求得全反射的临界角;由几何关系可求得光点到O′之间的距离.
(2)使玻璃砖绕圆心O点顺时针转动,相当于玻璃砖不动,入射光线逆时针,出射光线也逆时针转动,可知光点向右移动.由全反射知识及几何知识可求得全反射的临界角;由几何关系可求得光点到O′之间的距离.
解答:解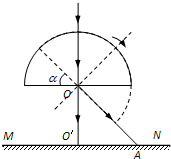 :(1)A、根据相邻波峰或波谷间的距离等于波长,读出两列波的波长都为λ=2cm.故A正确.
:(1)A、根据相邻波峰或波谷间的距离等于波长,读出两列波的波长都为λ=2cm.故A正确.
B、波速是由介质决定的,可知两列波的波速相等,由波速公式v=λf分析得知,两列波的频率相等.故B错误.
C、两波振幅不等,但频率相等,满足干涉的条件,故两列波相遇时会发生干涉现象.故C错误.
D、由于波速相等,所以两列波同时传到坐标原点.故D正确.
E、甲波向左传播,图中x=0.5cm处质点的振动方向沿+y轴方向,所以x=0.2cm处的质点开始振动时的方向向+y方向.故E错误.
F、两列波相遇时会发生干涉,两列波的波谷或波峰同时传播x=0.5cm处,则该处是振动加强的点.故F正确.
故答案为ADF
(2)使玻璃砖绕圆心O点顺时针转动,光屏上的光点将向右移动.
设玻璃砖转过α角时光点离O′点最远,记此时光点位置为A,此时光线在玻璃砖的平面上恰好发生全反射,临界角为C.
由折射定律有 sinC=
由几何关系知,全反射的临界角C=α=45°
光点A到O′的距离xAO′=
=h=10cm
故答案为:(1)ADF
(2)光屏上的光点将向右移动,光点离O′点最远是10c.
 :(1)A、根据相邻波峰或波谷间的距离等于波长,读出两列波的波长都为λ=2cm.故A正确.
:(1)A、根据相邻波峰或波谷间的距离等于波长,读出两列波的波长都为λ=2cm.故A正确.B、波速是由介质决定的,可知两列波的波速相等,由波速公式v=λf分析得知,两列波的频率相等.故B错误.
C、两波振幅不等,但频率相等,满足干涉的条件,故两列波相遇时会发生干涉现象.故C错误.
D、由于波速相等,所以两列波同时传到坐标原点.故D正确.
E、甲波向左传播,图中x=0.5cm处质点的振动方向沿+y轴方向,所以x=0.2cm处的质点开始振动时的方向向+y方向.故E错误.
F、两列波相遇时会发生干涉,两列波的波谷或波峰同时传播x=0.5cm处,则该处是振动加强的点.故F正确.
故答案为ADF
(2)使玻璃砖绕圆心O点顺时针转动,光屏上的光点将向右移动.
设玻璃砖转过α角时光点离O′点最远,记此时光点位置为A,此时光线在玻璃砖的平面上恰好发生全反射,临界角为C.
由折射定律有 sinC=
| 1 |
| n |
由几何关系知,全反射的临界角C=α=45°
光点A到O′的距离xAO′=
| h |
| tanα |
故答案为:(1)ADF
(2)光屏上的光点将向右移动,光点离O′点最远是10c.
点评:第1题考查对波动图象和波叠加原理的理解.第2题考查了光的折射定律,以及全反射等知识,对数学几何能力的要求较高,需加强训练.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 [物理----选修3-5]
[物理----选修3-5]






















