题目内容
3.某人造地球卫星绕地球铸匀速圆周运动,实施变轨后卫星的线速度减小到原来的$\frac{1}{2}$,此时卫星仍做匀速圆周运动,则( )| A. | 卫星的向心加速度减小到原来的$\frac{1}{4}$ | |
| B. | 卫星的角速度减小到原来的$\frac{1}{2}$ | |
| C. | 卫星的周期增大到原来的8倍 | |
| D. | 卫星圆周运动半径增大到原来的2倍 |
分析 万有引力提供圆周运动向心力由线速度变化求得轨道半径的变化,再根据轨道半径的变化求描述圆周运动物理量的变化.
解答 解:根据万有引力提供圆周运动向心力有$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}$可得卫星的线速度$v=\sqrt{\frac{GM}{r}}$,由此可知当卫星的线速度减小到原来的$\frac{1}{2}$,此时卫星的轨道半径增大为原来的4倍;再根据万有引力提供圆周运动向心力$G\frac{mM}{{r}^{2}}=ma=mr{ω}^{2}=mr\frac{4{π}^{2}}{{T}^{2}}$有:
A、a=$\frac{GM}{{r}^{2}}$可得向心加速度是原来的$\frac{1}{16}$,故A错误;
B、$ω=\sqrt{\frac{GM}{{r}^{3}}}$可得角速度是原来的$\frac{1}{8}$,故B错误;
C、由B知,周期是原来的8倍,故C正确;
D、轨道半径是原来的4倍,故D错误.
故选:C.
点评 能根据万有引力提供圆周运动向心力由线速度的变化确定轨道半径的变化,再根据轨道半径的关系求其它描述圆周运动物理量的关系是正确解题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
5. 如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )
如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )
 如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )
如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则( )| A. | 小球A与B之间库仑力的大小为$\frac{k{q}^{2}}{{d}^{2}}$ | |
| B. | 当$\frac{q}{d}$=$\sqrt{\frac{mgsinθ}{k}}$时,细线上的拉力为0 | |
| C. | 当$\frac{q}{d}$=$\sqrt{\frac{mgtanθ}{k}}$时,细线上的拉力为0 | |
| D. | 当$\frac{q}{d}$=$\sqrt{\frac{mg}{ktanθ}}$时,斜面对小球A的支持力为0 |
6.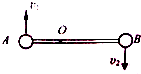 如图所示,两个小球固定在一杠杆两端,杠杆绕O点旋转,已知OA:OB=1:2,小球A的线速度大小为v1,角速度为ω1,周期为T1,向心加速度为α1;小球B的线速度大小为v2,角速度为ω2,周期为T2,向心加速度为α2.则( )
如图所示,两个小球固定在一杠杆两端,杠杆绕O点旋转,已知OA:OB=1:2,小球A的线速度大小为v1,角速度为ω1,周期为T1,向心加速度为α1;小球B的线速度大小为v2,角速度为ω2,周期为T2,向心加速度为α2.则( )
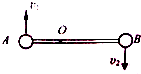 如图所示,两个小球固定在一杠杆两端,杠杆绕O点旋转,已知OA:OB=1:2,小球A的线速度大小为v1,角速度为ω1,周期为T1,向心加速度为α1;小球B的线速度大小为v2,角速度为ω2,周期为T2,向心加速度为α2.则( )
如图所示,两个小球固定在一杠杆两端,杠杆绕O点旋转,已知OA:OB=1:2,小球A的线速度大小为v1,角速度为ω1,周期为T1,向心加速度为α1;小球B的线速度大小为v2,角速度为ω2,周期为T2,向心加速度为α2.则( )| A. | v1:v2=1:2 | B. | ω1:ω2=1:2 | C. | T1:T2=1:2 | D. | α1:α2=1:4 |
13.下列说法正确的是( )
| A. | 电子伏特是电势能或电场力做功的单位,1电子伏特就是1焦耳 | |
| B. | 场强单位可以写成C/m2,也可以写作v/m | |
| C. | 带电微粒所带的电荷量不可能是-2.4×10-19C | |
| D. | 带电体所带最小电荷量叫做元电荷,为1C |
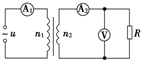 如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=220匝,交流电源的电压u=220$\sqrt{2}$sin100πt(V).电阻R=44Ω,电压表、电流表为理想电表,则交流电的频率为50Hz,电流表
如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=220匝,交流电源的电压u=220$\sqrt{2}$sin100πt(V).电阻R=44Ω,电压表、电流表为理想电表,则交流电的频率为50Hz,电流表 的示数为0.2A,电流表
的示数为0.2A,电流表 的示数为1A,电压表的示数为44V.
的示数为1A,电压表的示数为44V. 质量为10kg的物质在F=200N与斜面平行的力作用下,从粗糙斜面的底端由静止开始沿斜面向上运动,斜面固定不动且足够长,斜面与水平地面的夹角θ=37°.力F作用2s后撤去,物体在斜面上继续上滑了3s后,速度减为零.求:
质量为10kg的物质在F=200N与斜面平行的力作用下,从粗糙斜面的底端由静止开始沿斜面向上运动,斜面固定不动且足够长,斜面与水平地面的夹角θ=37°.力F作用2s后撤去,物体在斜面上继续上滑了3s后,速度减为零.求: 如图所示,平行放置的金属板A、B组成一个平行板电容器.
如图所示,平行放置的金属板A、B组成一个平行板电容器. 如图所示,一质量为m带正电的小球,用长为L的绝缘细线悬挂于O点,处于一水平方向的匀强电场中,静止时细线右偏与竖直方向成45°角,位于图中的P点.重力加速度为g.求:
如图所示,一质量为m带正电的小球,用长为L的绝缘细线悬挂于O点,处于一水平方向的匀强电场中,静止时细线右偏与竖直方向成45°角,位于图中的P点.重力加速度为g.求: