题目内容
（20分）在光滑水平地面上有一凹槽A，中央放一小物块B，物块与左右两边槽壁的距离如图所示，L为1.0m，凹槽与物块的质量均为m，两者之间的动摩擦因数μ为0.05，开始时物块静止，凹槽以v0＝5m/s初速度向右运动，设物块与凹槽槽壁碰撞过程中没有能量损失，且碰撞时间不计。g取10m/s2。求：( )
（1）物块与凹槽相对静止时的共同速度；
（2）从凹槽开始运动到两者相对静止物块与右侧槽壁碰撞的次数；
（3）从凹槽开始运动到两者刚相对静止所经历的时间及该时间内凹槽运动的位移大小。
（1）v=2.5m/s；（2）6次；（3）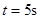
，
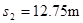
解析试题分析：（1）设两者间相对静止时速度为v，由动量守恒定律得mv0=2mv，可得v=2.5m/s
（2）物块与凹槽间的滑动摩擦力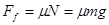 
设两者间相对静止前相对运动的路程是s1，由动能定理得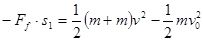
得 
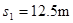
已知L=1m可推知物块与右侧槽壁共发生6次碰撞。
（3）设凹槽与物块碰撞前的速度分别为v1、v2，碰后的速度分别为v1′、v2′，有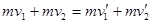
得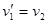 
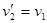
即每碰撞一次凹侧与物块发生一次速度交换，在同一坐标系上两者的速度图线如图所示：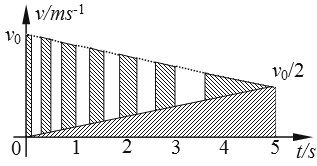
根据碰撞次数可分为13段，凹槽、物块的v-t图象在两条连续的匀变速运动图线间转换，故可用匀变速直线运动规律求时间。则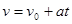
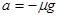
解得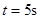
凹槽的v-t图象所包围的阴影部分面积即为凹槽的位移大小s2，（等腰三角形面积共13份，第一份面积为0.5L，其余每份面积均为L。）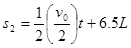
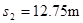
考点：动量守恒定律、运动学的基本规律
练习册系列答案
相关题目
（10分）一个小球沿斜面向下运动，现在用
的闪频相机拍摄下的不同时刻的小球所处的位置照片如图所示，测得小球的在连续相等的时间内的位移如下表，则：
 |  |  |  |
| 8.20cm | 9.30cm | 10.40cm | 11.50cm |
（2）有甲、乙两个同学计算小球的加速度的方法如下：
甲：
，
，
，
；乙：
，
，
；撇开本题所给的数据从理论上讲，甲、乙两位同学的计算方法中 （填写“甲、乙”）方法更好，本题中小球的加速度值为 m/s2，求经过A点处速度为__________m/s。 
的固定斜面，斜面上放一质量为m的光滑球。静止时，箱子顶部与球接触但无压力。箱子由静止开始向右做匀加速运动，然后改做加速度大小为a的匀减速运动直至静止，经过的总路程为s，运动过程中的最大速度为v。
