Question

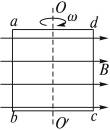
如图17-1-19所示，正方形线圈abcd绕对称轴OO′在匀强磁场中匀速转动，转动次数n=120 min^-1.若已知ab=bc=20 cm，匝数=20，磁感应强度B=0.2 T，求：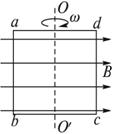

图17-1-19

（1）转动中最大电动势位置；

（2）从图示位置转过90°过程中的平均电动势；

（3）设线圈是闭合的，总电阻R=10 Ω，线圈转动过程中受到的最大电磁力矩及位置.

Answer 1

解析：平均电动势由法拉第电磁感应定律求解，最大磁力矩对应着感应电流的最大位置.

（1）N匝线圈转动中的最大电动势为ε_m=NBSω?

式中ω=2πf=2π×rad/s=4 rad/s

代入各已知数据得：ε_m=20×0.2×0.2×0.2×4πV=2.01V

与最大电动势所对应的线圈位置如图中所示，即垂直中性面的位置.?

（2）图示位置转过90°过程中，线圈中发生的磁通量变化ΔΦ=BS，历时，由法拉第电磁感应定律得平均电动势4×20×0.2×0.2×0.2×2 V=1.28 V.?

（3）线圈转动时产生感应电动势，激起感应电流，使线圈受到一个与外力矩方向相反的磁力矩M=NBIS，它也是一个随时间变化的量，最大磁力矩对应于感应电动势（或感应电流）有最大值的位置，其值为M_m=NBI_mS=NBS=0.032 N·m.