题目内容
6. 竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率vc=$\sqrt{\frac{4gR}{5}}$,则下述不正确的是( )
竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率vc=$\sqrt{\frac{4gR}{5}}$,则下述不正确的是( )| A. | 小球到达C点时对轨道的压力是$\frac{4mg}{5}$ | |
| B. | 此球的最大速率是$\sqrt{6}$vc | |
| C. | 小球在任一直径两端点上的动能之和相等 | |
| D. | 小球沿圆轨道绕行一周所用的时间等于$π\sqrt{\frac{5R}{g}}$ |
分析 因为圆环轨道是光滑的,只有重力做功,所以机械能守恒,可以求得在最低点时的最大速度;
对物体受力分析,根据圆周运动的向心力公式可以求得对轨道的作用力,由周期公式可以知道物体运动的周期.
解答 解:A、在C点有:mg-N=m$\frac{{v}_{C}^{2}}{R}$,得:N=$\frac{1}{5}$mg,小球到达C点时对轨道的压力为:N′=N=$\frac{1}{5}$mg,故A错误.
B、速度最大的点应该是最低点时,根据机械能守恒得:$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}$mvc2=2mgR,解得最大速率为:v=$\sqrt{\frac{24gR}{5}}$=$\sqrt{6}$vc,故B正确.
B、整个过程中机械能守恒,在任一直径两端点上的点,它们的高度之和都是2R,即它们的重力势能的和相等,由于总的机械能守恒,所以它们的动能之和也相等,故C正确.
C、D、由周期T=$\frac{2πR}{v}$,当圆环以速度最小vc=$\sqrt{\frac{4gR}{5}}$做匀速圆周运动时周期最小,vc=$\sqrt{\frac{4gR}{5}}$代入T=$\frac{2πR}{v}$,计算可得T=π$\sqrt{\frac{5R}{g}}$,由于小球离开最高点后速度在变大,所以T要减小,所以T<T=π$\sqrt{\frac{5R}{g}}$,故D错误.
本题选错误的,故选:AD.
点评 小球穿在圆环轨道上做圆周运动,属于杆的模型,在最高点时速度最小,向心力最小,最低点时速度最大,向心力最大,由机械能守恒可以求它们之间的关系.

练习册系列答案
相关题目
16. 如图所示,在水平地面上M点的正上方某一高度处,将S1球以初速度v1水平向右抛出,同时在M点右方地面上N点处,将S2球以初速度v2斜向左上方抛出,两球恰在M、N连线的中点正上方相遇,不计空气阻力,则两球从抛出到相遇过程中( )
如图所示,在水平地面上M点的正上方某一高度处,将S1球以初速度v1水平向右抛出,同时在M点右方地面上N点处,将S2球以初速度v2斜向左上方抛出,两球恰在M、N连线的中点正上方相遇,不计空气阻力,则两球从抛出到相遇过程中( )
 如图所示,在水平地面上M点的正上方某一高度处,将S1球以初速度v1水平向右抛出,同时在M点右方地面上N点处,将S2球以初速度v2斜向左上方抛出,两球恰在M、N连线的中点正上方相遇,不计空气阻力,则两球从抛出到相遇过程中( )
如图所示,在水平地面上M点的正上方某一高度处,将S1球以初速度v1水平向右抛出,同时在M点右方地面上N点处,将S2球以初速度v2斜向左上方抛出,两球恰在M、N连线的中点正上方相遇,不计空气阻力,则两球从抛出到相遇过程中( )| A. | 初速度大小关系为v1=v2 | B. | 速度变化量相等 | ||
| C. | 都是变加速运动 | D. | 都不是匀变速运动 |
17. 如图所示,A、B是被绝缘支架分别架起的金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )
如图所示,A、B是被绝缘支架分别架起的金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )
 如图所示,A、B是被绝缘支架分别架起的金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )
如图所示,A、B是被绝缘支架分别架起的金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )| A. | 导体B带负电 | |
| B. | 导体B左端出现负电荷,右端出现正电荷,并且电荷量大小相等 | |
| C. | 若A不动,将B沿图中虚线分开,则两边的电荷量大小相等,与如何分无关 | |
| D. | 只要A与B不接触,B的总电荷量总是为零 |
14. 如图所示,物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2m,BC=3m,且物体通过AB、BC、CD所用的时间相等,则下列说法正确的是( )
如图所示,物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2m,BC=3m,且物体通过AB、BC、CD所用的时间相等,则下列说法正确的是( )
 如图所示,物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2m,BC=3m,且物体通过AB、BC、CD所用的时间相等,则下列说法正确的是( )
如图所示,物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2m,BC=3m,且物体通过AB、BC、CD所用的时间相等,则下列说法正确的是( )| A. | 可以求出物体加速度的大小 | B. | 可以求得CD=4m | ||
| C. | 可以求得OA之间的距离为1.125m | D. | 可以求得OA之间的距离为1m |
1. 如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
 如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )| A. | a的水平速度比b的小 | B. | a的飞行时间比b的长 | ||
| C. | b和c的飞行时间相同 | D. | b的初速度比c的大 |
11.下列说法正确的是( )
| A. | 运动得越快的汽车越不容易停下来,是因为汽车运动得越快,惯性越大 | |
| B. | 不管物体匀速运动时,还是变速运动时,都存在惯性 | |
| C. | 只有静止的物体受到的摩擦力才叫静摩擦力 | |
| D. | 滑动摩擦力不可能是物体运动的动力 |
15.(多选)在运用图所示装置做“探究功与速度变化的关系”的实验中,下列说法正确的是( )
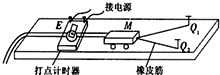

| A. | 通过改变橡皮筋的条数改变拉力做功的数值 | |
| B. | 由于本实验中的摩擦力较小,所以没必要平衡摩擦力 | |
| C. | 通过打点计时器打下的纸带来测定小车加速过程中获得的最大速度 | |
| D. | 通过打点计时器打下的纸带来测定小车加速过程中获得的平均速度 |
12.在光滑水平面上和粗糙水平面上水平施加力推小车,如果所用的推力相等、位移也相等,则推力对小车做的功是( )
| A. | 在粗糙水平面上的较大 | |
| B. | 在光滑水平面上的较大 | |
| C. | 两种情况下推力做的功相等 | |
| D. | 做功的大小决定于两车通过该位移的时间 |
 在用重锤下落来验证机械能守恒时,某同学按照正确的操作选的纸带如图所示.其中O是起始点,A、B、C、D、E是打点计时器连续打下的5个点,打点频率为50Hz,该同学用毫米刻度尺测量O到A、B、C、D、E各点的距离,并记录在图中(单位:cm)
在用重锤下落来验证机械能守恒时,某同学按照正确的操作选的纸带如图所示.其中O是起始点,A、B、C、D、E是打点计时器连续打下的5个点,打点频率为50Hz,该同学用毫米刻度尺测量O到A、B、C、D、E各点的距离,并记录在图中(单位:cm)