题目内容
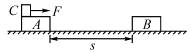
如图1-8-5所示,两个完全相同的质量为m的木板A、B置于水平地面上,它们的间距s=2.88 m.质量为2m、大小可忽略的物块C置于A板的左端.C与A之间的动摩擦因数为μ1=0.22,A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给C施加一个水平向右、大小为
图1-8-5
解析:设A、C之间的滑动摩擦力大小为Fμ1,A与水平地面之间的滑动摩擦力大小为Fμ2.
因为μ1=0.22,μ2=0.10
所以F=![]() mg<Fμ1=μ12mg
mg<Fμ1=μ12mg
且F=![]() mg>Fμ2=μ2(2m+m)g
mg>Fμ2=μ2(2m+m)g
所以一开始A和C保持相对静止,在F的作用下向右加速运动,有(F-Fμ2)·s=![]() ·(2m+m)v12
·(2m+m)v12
A、B两木板的碰撞瞬间,内力的冲量远大于外力的冲量,由动量守恒定律得
mv1=(m+m)v2
碰撞结束后到三个物体达到共同速度的相互作用过程中,设木板向前移动的位移为s1.选三个物体构成的整体为研究对象,外力之和为零,则
2mv1+(m+m)v2=(2m+m+m)v3
设A、B系统与水平地面之间的滑动摩擦力大小为![]() ,对A、B系统,由动能定理
,对A、B系统,由动能定理
![]() ·s1-
·s1-![]() ·S1=
·S1=![]() ·2mv32-
·2mv32-![]() ·2mv22,
·2mv22,![]() =μ2(2m+m+m)g
=μ2(2m+m+m)g
对C物体,由动能定理F·(2l+s1)-![]() ·(2l+s1)=
·(2l+s1)=![]() 2mv32-
2mv32-![]() 2mv12
2mv12
由以上各式,再代入数据可得l=0.3 m.
答案:l=0.3 m

练习册系列答案
相关题目