题目内容
6. 如图所示,一个小球质量为m,在A点的动能为3mgR,沿粗糙的水平面向右运动,冲上半径为R的光滑圆弧轨道,恰好能通过圆弧的最高点,则小球在水平面内克服摩擦力所做的功( )
如图所示,一个小球质量为m,在A点的动能为3mgR,沿粗糙的水平面向右运动,冲上半径为R的光滑圆弧轨道,恰好能通过圆弧的最高点,则小球在水平面内克服摩擦力所做的功( )| A. | mgR | B. | 2mgR | C. | 0.5mgR | D. | 3mgR |
分析 小球恰好能通过圆弧的最高点时,由重力充当向心力,由牛顿第二定律求小球通过最高点C时的速度.再对A到C的过程,运用动能定理求小球在水平面内克服摩擦力所做的功.
解答 解:小球恰好能通过圆弧的最高点时,由重力充当向心力,由牛顿第二定律得:
mg=m$\frac{{v}_{C}^{2}}{R}$ ①
从A到C过程,由动能定理有:
-2mgR-Wf=$\frac{1}{2}m{v}_{C}^{2}$-EkA ②
据题,EkA=2mgR ③
联立①②③解得:Wf=0.5mgR
故选:C
点评 解决本题的关键要把握圆周运动最高点的临界条件:重力等于向心力,知道动能定理是求变力做功常用的方法.

练习册系列答案
相关题目
12.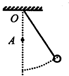 如图所示,细绳的一端悬于O点,另一端系一小球,在O点正下方A处 有一钉子.现使小球由高处摆下,当绳摆到竖直位置时与钉子相碰.则绳碰钉子前后的瞬间相比(不计空气阻力)( )
如图所示,细绳的一端悬于O点,另一端系一小球,在O点正下方A处 有一钉子.现使小球由高处摆下,当绳摆到竖直位置时与钉子相碰.则绳碰钉子前后的瞬间相比(不计空气阻力)( )
 如图所示,细绳的一端悬于O点,另一端系一小球,在O点正下方A处 有一钉子.现使小球由高处摆下,当绳摆到竖直位置时与钉子相碰.则绳碰钉子前后的瞬间相比(不计空气阻力)( )
如图所示,细绳的一端悬于O点,另一端系一小球,在O点正下方A处 有一钉子.现使小球由高处摆下,当绳摆到竖直位置时与钉子相碰.则绳碰钉子前后的瞬间相比(不计空气阻力)( )| A. | 小球的线速度变大 | B. | 小球的角速度不变 | ||
| C. | 小球的向心加速度减小 | D. | 绳子的拉力变大 |
14. 2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
 2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )| A. | “火星合日”约每1年出现一次 | |
| B. | “火星合日”约每4年出现一次 | |
| C. | 火星的公转半径约为地球公转半径的$\root{3}{4}$倍 | |
| D. | 火星的公转半径约为地球公转半径的8倍 |
1.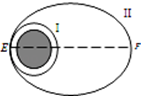 今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
 今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )
今年5月,信使号水星探测器陨落在水星表面.之前,工程师通过向后释放推进系统中的高压氦气来提升轨道,使其寿命再延长一个月,如图所示,释放氦气前,探测器在贴近水星表面的圆形轨道Ⅰ上做匀速圆周运动,释放氦气后探测器进入椭圆轨道Ⅱ,忽略探测器在椭圆轨道上所受阻力.则下列说法正确的是( )| A. | 探测器在轨道I的运行周期比在轨道Ⅱ的大 | |
| B. | 探测器在轨道Ⅱ上某点的速率可能等于在轨道Ⅰ上速率 | |
| C. | 探测器在轨道Ⅰ和轨道Ⅱ上的E处加速度相同 | |
| D. | 探测器在轨道Ⅱ上远离水星过程中,势能和动能均增大 |
11. 阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
 阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )| A. | 电极A1的电势高于电极A2的电势 | |
| B. | 电场中Q点的电场强度小于R点的电场强度 | |
| C. | 电子在R点处的动能小于在P点处的动能 | |
| D. | 若将一束带正电的粒子从左侧射入聚焦电场也一定被会聚 |
18.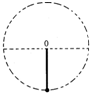 为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )
为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )
 为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )
为了测量某行星的质量和半径,宇航员记录了登陆舱在该行星表面做圆周运动的周期T,登陆舱在行星表面着陆后,用弹簧称称量一个质量为m的砝码读数为N.已知引力常量为G.则下列计算中正确的是( )| A. | 在该行星的第一宇宙速度为$\frac{NT}{2πm}$ | B. | 该行星的密度为$\frac{3G}{{π{T^2}}}$ | ||
| C. | 该行星的质量为$\frac{{N}^{3}{T}^{4}}{16{π}^{4}{m}^{3}}$ | D. | 该行星的半径为$\frac{4{π}^{2}N{T}^{2}}{m}$ |
16.如图,用手紧握住一个油瓶,并使瓶始终处于竖直方向,下列说法正确的是( )
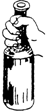

| A. | 瓶中油越多,手必须握得越紧 | |
| B. | 手握得越紧,油瓶受到的摩擦力越大 | |
| C. | 不管手握得有多紧,油瓶受到的摩擦力大小总是一定的 | |
| D. | 油瓶所受摩擦力为滑动摩擦力 |
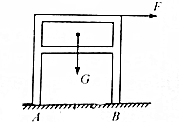 如图所示,桌子在水平力F的作用下匀速缓慢移动,已知桌子重G=100N,桌腿与地面的摩擦系数μ=0.2,桌子的宽、高相等.求:
如图所示,桌子在水平力F的作用下匀速缓慢移动,已知桌子重G=100N,桌腿与地面的摩擦系数μ=0.2,桌子的宽、高相等.求: 如图所示,带电粒子以某一初速度进入一垂直于纸面向里、磁感应强度为B的有界匀强磁场,粒子垂直进入磁场时的速度与水平方向成θ=60°角,接着垂直进入电场强度大小为E、水平宽度为L、方向竖直向上的匀强磁场,粒子穿出电场时速度大小变为原来的$\sqrt{2}$倍.已知带电粒子的质量为m、电荷量为q,重力不计.
如图所示,带电粒子以某一初速度进入一垂直于纸面向里、磁感应强度为B的有界匀强磁场,粒子垂直进入磁场时的速度与水平方向成θ=60°角,接着垂直进入电场强度大小为E、水平宽度为L、方向竖直向上的匀强磁场,粒子穿出电场时速度大小变为原来的$\sqrt{2}$倍.已知带电粒子的质量为m、电荷量为q,重力不计.