题目内容
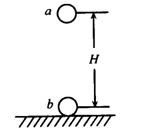
如图，两个完全相同的弹性小球A和B分别悬挂在两根长度分别为L和4L的不可伸长的轻绳末端，两绳均处于竖直状态，两小球重心在同一水平线上且刚好相互接触，现将A球拉到一个很小的角度由静止释放，则在A球运动的2个周期内，两球相碰的次数为（ ）分析：根据单摆的周期公式T=2π
得出两球的周期比，两球发生弹性碰撞，质量相等，根据动量守恒定律和能量守恒定律，两球相碰后交换速度，从而得出A球运动的2个周期内，两球相碰的次数．
|
解答：解：根据单摆的周期公式T=2π
得，摆长比为1：4，则周期比为1：2．两球发生弹性碰撞，质量相等，根据动量守恒定律和能量守恒定律，两球相碰后交换速度，A球运动2个周期，B球运动了一个周期，知在这段时间内两球相碰的次数为3次．故C正确，A、B、D错误．
故选C．
|
故选C．
点评：解决本题的关键掌握单摆的周期公式，以及知道弹性碰撞的过程中，动量守恒，能量守恒．
练习册系列答案
阅读快车系列答案
相关题目
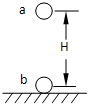如图有两个完全相同的金属球a、b，b固定在绝缘地板上，a在离b高H的正上方，由静止释放与b发生碰撞后回跳高度为h．设碰撞中无动能损失，空气阻力不计，则（ ）| A、若a、b带等量同种电荷，则H＞h | B、若a、b带等量同种电荷，则H＜h | C、若a、b带等量异种电荷，则H＜h | D、若a、b带等量异种电荷，则H=h |
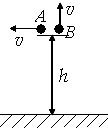如图，两个完全相同的小球A、B，在同一高度处以相同大小的初速度v分别水平抛出和竖直向上抛出，下列说法正确的是（ ）| A、两小球落地时的速度相同 | B、两小球落地时，A球重力的瞬时功率较小 | C、从开始运动至落地，A球重力做功较大 | D、从开始运动至落地，重力对A小球做功的平均功率较小 |
