题目内容
(2005年广东)如图所示,两个完全相同的质量为m的木板A、B置于水平地面上,它们的间距s=2.88m.质量为2m、大小可忽略的物块C置于A板的左端.C与A之间的动摩擦因数为 ,A、B与水平地面之间的动摩擦因数为
,A、B与水平地面之间的动摩擦因数为 ,最大静摩擦力可认为等于滑动摩擦力,开始时,三个物体处于静止状态.现给C施加一个水平向右,大小为
,最大静摩擦力可认为等于滑动摩擦力,开始时,三个物体处于静止状态.现给C施加一个水平向右,大小为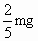 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,要使C最终不脱离木板,每块木板的长度至少应为多少?
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,要使C最终不脱离木板,每块木板的长度至少应为多少?

答案:0.3m
解析:
解析:
|
命题目的:本题涉及牛顿第二定律、动能定理、动量守恒定律、功能关系等知识点,把力与运动、动量和能量紧密联系起来,求解本题的关键是认真分析不同物理过程中物体的受力情况,以确定物体的运动规律,在用动量和能量列方程时,要注意对参照物的选取,本题很好地考查了考生分析、推理和综合能力. 解析:设 A、C之间的滑动摩擦力大小为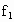 ,A与水平地面之间的滑动摩擦力大小为 ,A与水平地面之间的滑动摩擦力大小为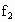 . .
A、B两木板的碰撞瞬间,内力的冲量远大于外力的冲量,由动量守恒定律得:(特别注意木块C没有参与碰撞)
碰撞结束后三个物体达到共同速度的相互作用过程中,设木板向前移动的位移为
设A、B系统与水平地面之间的滑动摩擦力大小为
对C物体,由动能定理
由以上各式再代入数据可得 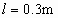 . . |

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
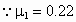 ,
,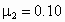 ,
,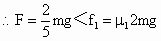 且
且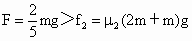 .
.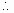 一开始A和C保持相对静止,在F的作用下向右加速运动,有
一开始A和C保持相对静止,在F的作用下向右加速运动,有 .
.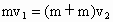 .
.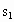 ,选三个物体构成的整体为研究对象,系统水平方向所受外力
,选三个物体构成的整体为研究对象,系统水平方向所受外力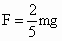 和
和 ,外力之和为零,则系统动量守恒
,外力之和为零,则系统动量守恒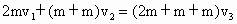 .
.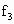 ,对A、B系统,由动能定理,
,对A、B系统,由动能定理,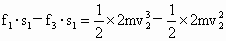 ,
,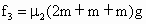 .
.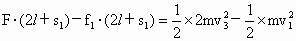 .
.