Question

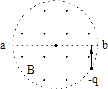
【题目】如图所示，一个绝缘光滑半圆环轨道放在竖直向下的匀强电场E中，在环的上端，一个质量为m、带电荷量为+q的小球由静止开始 沿轨道运动，则（ ）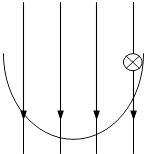

A.小球运动过程中机械能守恒
B.小球经过环的最低点时速度最小
C.在最低点球对环的压力为（mg+qE）
D.在最低点球对环的压力为3（mg+qE）

Answer 1

【答案】D
【解析】解：
A、小球运动过程中电场力做功，机械能不守恒．故A错误．
B、小球从最高点到最低点的过程中，合力做正功，则根据动能定理得知，动能增加，速率增大，所以小球经过环的最低点时速度最大．故B错误．
C、D小球从最高点到最低点的过程，根据动能定理得：（mg+qE）R= 又由N﹣mg﹣qE= ，联立解得N=3（mg+qE）．故C错误，D正确．
故选D
【考点精析】利用向心力和动能定理的综合应用对题目进行判断即可得到答案，需要熟知向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力；应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．