题目内容
如图所示,在竖直向下,场强为E的匀强电场中,长为l的绝缘轻杆可绕固定轴O在竖直面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为m1和m2(m1<m2),A带负电,电量为q1,B带正电,电量为q2。杆从静止开始由水平位置转到竖直位置,求: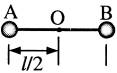
【小题1】在此过程中电场力所做的功为多少?
【小题2】在竖直位置处两球的总动能为多少?
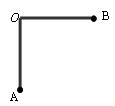
若将轻杆弯折成如图所示的“Γ”形,两边互相垂直、长度均为l/2 ,两端各固定一个金属小球A、B,在竖直向下,场强为E的匀强电场中,可绕过O点的水平轴在竖直平面内无摩擦转动。已知A球质量m1=m,电量为+q,B球质量m2=7m/2,B球也带负电,电量为-q。现将“Γ”形杆从OB位于水平位置由静止释放,求:
【小题3】OB杆能转过的最大角度为127°,则该电场强度的大小为多少?
【小题4】当两球的速度达到最大时,OB杆转过的角度为多大?
【小题1】WE=q2EL/2+q1EL/2=(q1+q2)EL/2
【小题2】WG=m2gL/2-m1gL/2=(m2-m1)gL/2,Ek=WE+WG=(q1E+q2E+m2g-m1g)L/2
【小题3】0.35mg´0.8´L/2-mg´1.6´L/2-qE´0.8´L/2-qE´1.6´L/2=0,E=mg/2q
【小题4】速度达到最大时力矩平衡,设转过的角度为q,(qE+mg)sinq=(0.35mg-qE)cosq,tanq=2
解析

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 如图所示,在竖直向下场强大小为E的匀强电场中,有一光滑绝缘半圆环在其上端一个质量为m、带电量为+q的小球由静止开始沿轨道运动,则( )
如图所示,在竖直向下场强大小为E的匀强电场中,有一光滑绝缘半圆环在其上端一个质量为m、带电量为+q的小球由静止开始沿轨道运动,则( ) 如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m=1kg,电量大小为q=6×10-4C,匀强电场的场强大小为E=1×104N/C,斜轨道的倾角为α=30°,圆轨道半径R=0.8m,(小球的重力大于所受的电场力g=10m/s2).
如图所示,在竖直向下的匀强电场中有一绝缘的光滑离心轨道,一个带负电的小球从斜轨道上的A点由静止释放,沿轨道滑下,已知小球的质量为m=1kg,电量大小为q=6×10-4C,匀强电场的场强大小为E=1×104N/C,斜轨道的倾角为α=30°,圆轨道半径R=0.8m,(小球的重力大于所受的电场力g=10m/s2). 如图所示,在竖直向下的匀强磁场中,将一个水平放置的金属棒ab以水平初速度V0抛出,设运动的整个过程中棒的取向不变且不计空气阻力,则金属棒在运动过程中产生的感应电动势大小将( )
如图所示,在竖直向下的匀强磁场中,将一个水平放置的金属棒ab以水平初速度V0抛出,设运动的整个过程中棒的取向不变且不计空气阻力,则金属棒在运动过程中产生的感应电动势大小将( ) (2009?奉贤区二模)如图所示,在竖直向下的匀强磁场中,有两根竖直放置的平行导轨AB、CD,导轨上放有质量为m的金属棒MN,棒与导轨间的动摩擦因数为u,现从t=0时刻起,给棒通以图示方向的电流,且电流强度与时间成正比,即I=kt,其中k为恒量.若金属棒与导轨始终垂直,则下图所示的表示棒所受的摩擦力随时间变化的四幅图中,正确的是( )
(2009?奉贤区二模)如图所示,在竖直向下的匀强磁场中,有两根竖直放置的平行导轨AB、CD,导轨上放有质量为m的金属棒MN,棒与导轨间的动摩擦因数为u,现从t=0时刻起,给棒通以图示方向的电流,且电流强度与时间成正比,即I=kt,其中k为恒量.若金属棒与导轨始终垂直,则下图所示的表示棒所受的摩擦力随时间变化的四幅图中,正确的是( )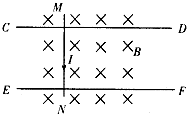 如图所示,在竖直向下的匀强磁场中有两根水平放置的平行粗糙导轨CD、EF,导轨上放有一金属棒MN.现从t=0时刻起,给棒通以图示方向的电流且电流强度与时间成正比,即I=kt,其中k为常量,金属棒与导轨始终垂直且接触良好.下列关于棒的速度v、加速度a随时间t变化的关系图象,可能正确的是( )
如图所示,在竖直向下的匀强磁场中有两根水平放置的平行粗糙导轨CD、EF,导轨上放有一金属棒MN.现从t=0时刻起,给棒通以图示方向的电流且电流强度与时间成正比,即I=kt,其中k为常量,金属棒与导轨始终垂直且接触良好.下列关于棒的速度v、加速度a随时间t变化的关系图象,可能正确的是( )