题目内容
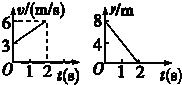 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,则该质点所受合外力为
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,则该质点所受合外力为分析:根据速度图象判断物体在x轴方向做匀加速直线运动,y轴做匀速直线运动.根据位移图象的斜率求出y轴方向的速度,再将两个方向的合成,求出合速度.根据斜率求出x轴方向的合力,即为质点的合力.
解答:解:物体在x轴方向做匀加速直线运动,y轴做匀速直线运动;
2s时刻x方向速度为6m/s,y轴方向速度vy=-4m/s,故合速度为:
v=
=
=2
m/s
x轴方向的加速度a=1.5m/s2,质点的合力F合=ma=3N
故答案为:3,2
m/s.
2s时刻x方向速度为6m/s,y轴方向速度vy=-4m/s,故合速度为:
v=
|
| 62+42 |
| 13 |
x轴方向的加速度a=1.5m/s2,质点的合力F合=ma=3N
故答案为:3,2
| 13 |
点评:本题考查运用运动合成与分解的方法处理实际问题的能力,类似平抛运动.中等难度.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
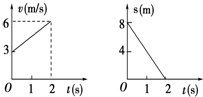 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( ) 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( ) 质量为2kg的质点在x一y平面内做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x一y平面内做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )